Đề bài

Cho tam giác $ABC$  có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$  và $ANC.$

• A. Ba điểm $M,A,N$ thẳng hàng.
• B. $BN = CM$
• C. Cả A, B đều sai
• D. Cả A, B đều đúng

Phương pháp giải :

+ Ta sử dụng tính chất tam giác cân, tính chất tia phân giác của một góc, tính chất hai góc kề bù để chứng minh các cặp góc so le trong bằng nhau để chứng minh ba điểm $M,A,N$ thẳng hàng.

+ Chứng minh cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.

Lời giải chi tiết :

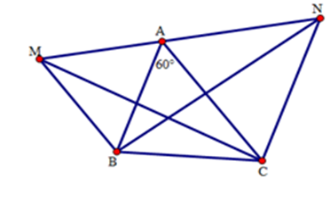
+  Các tam giác $AMB$ và $ANC$  là các tam giác đều(gt) nên \(\widehat {MAB} = {60^0},\,\,\,\widehat {NAC} = {60^0}\).

Ta có: \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = {60^0} + {60^0} + {60^0} = {180^0}.\)

Suy ra ba điểm $M,A,N$ thẳng hàng.

+  Ta có:

 $\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}$

Do đó \(\widehat {MAC} = \widehat {BAN}\) .

Xét hai tam giác $ABN$  và $AMC$  có:

+) $AB = AM$ (do tam giác $AMB$ đều)

+) \(\widehat {BAN} = \widehat {MAC}\) (cmt)

+) $AN = AC$ (do tam giác $ANC$ đều)

Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)

Suy ra $BN = CM$ (hai cạnh tương ứng).

Vậy cả A, B đều đúng.

Đáp án : D