Đề bài

Cho tam giác $ABC,D$ là trung điểm của $AB.$  Đường thẳng qua $D$  và song song với $BC$  cắt $AC$  ở $E,$  đường thẳng qua $E$  và song song với $AB$  cắt $BC$  ở $F.$ Khi đó

• A. $\Delta ADE = \Delta EFC$
• B. $\Delta ADE = \Delta DBF$                       
• C. $\Delta EFC = \Delta DBF$           
• D. Cả A, B, C đều đúng.

Phương pháp giải

+ Từ tính chất của hai đường song song suy ra các cặp góc bằng nhau, từ đó dựa vào trường hợp bằng nhau thứ ba của tam giác để chứng minh các tam giác bằng nhau

+ Từ các cặp cạnh bằng nhau ta tìm mối liên hệ giữa chúng để suy ra điều phải chứng minh

Lời giải của GV Loigiaihay.com

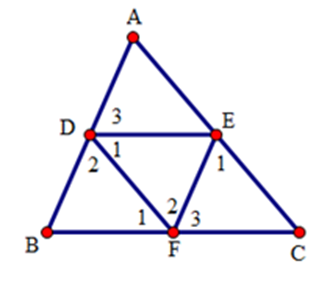
Xét tam giác $DEF$  và tam giác $FBD$  có:

$\widehat {{D_1}} = \widehat {{F_1}}$ (hai góc so le trong).

$DF$ là cạnh chung

$\widehat {{F_2}} = \widehat {{D_2}}$ (hai góc so le trong).

Vậy $\Delta DEF = \Delta FBD\,\,\,(g.c.g)$

Suy ra $EF = BD$ (hai cạnh tương ứng)

 Mà $AD = BD$ nên $EF = AD$

Ta có : $\widehat {{F_3}} = \widehat B$ (hai góc đồng vị); $\widehat {{D_3}} = \widehat B$ (hai góc đồng vị)

 $\Rightarrow \widehat {{D_3}} = \widehat {{F_3}}\left( { = \widehat B} \right).$.

Xét tam giác $ADE$ và tam giác $EFC$  có:

$\widehat {{D_3}} = \widehat {{F_3}}$(cmt)

$\widehat A = \widehat {{E_1}}$(hai góc đồng vị)

$AD = EF\left( {cmt} \right)$

 $\Rightarrow \Delta ADE = \Delta EFC\,\,\,(g.c.g).$  (1)

Tương tự ta chứng minh được $\Delta EFC = \Delta DBF\,\,\,(g.c.g)$     (2)

Từ (1) và (2) suy ra $\Delta ADE = \Delta EFC = \Delta DBF$                      (3)

Đáp án : D