Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm $O$ bán kính bằng $2cm,$ cung tròn này cắt $Ox, Oy$ lần lượt ở $A$ và $B.$ Vẽ các cung tròn tâm $A$ và tâm $B$ có bán kính $3cm,$ chúng cắt nhau tại điểm $C$ nằm trong góc $xOy.$ Tính \(\widehat {xOC}\) .
-
A.
\({25^0}\)
-
B.
\({50^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Ta chứng minh hai tam giác bằng nhau để suy ra hai góc tương ứng bằng nhau. Từ đó suy ra được điều phải chứng minh.
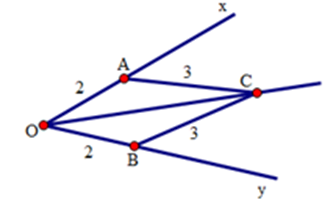
Xét hai tam giác $OAC$ và $OBC$ có:
$OA = OB = 2cm; OC$ là cạnh chung; $AC = BC = 3cm.$
Suy ra \(\Delta OAC = \Delta OBC(c.c.c)\)
Do đó \(\widehat {AOC} = \widehat {COB}\) (hai góc tương ứng).
Mà \(\widehat {AOC} + \widehat {COB} = {50^0}\) nên \(\widehat {AOC} = \widehat {COB} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Vậy \(\widehat {xOC} = {25^0}\).
Đáp án : A
Các bài tập cùng chuyên đề
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)
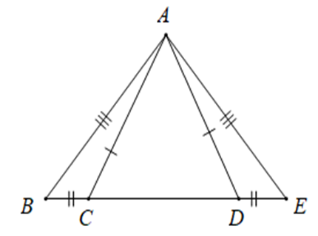
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai:
Cho hình dưới đây.
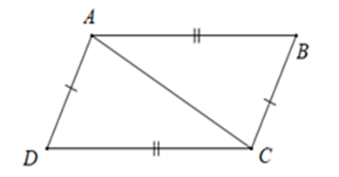
Chọn câu sai.
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
Cho tam giác $ABC$ có $AB = AC$ và $MB = MC$ (\(M \in BC\)). Chọn câu sai.
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
Cho tam giác $ABC$ có $AB < AC$ . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi $O$ là một điểm nằm ở trong tam giác sao cho $OA = OC,OB = OE.$ Khi đó:
