Cho tam giác $ABC$ có $AB < AC$ . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi $O$ là một điểm nằm ở trong tam giác sao cho $OA = OC,OB = OE.$ Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
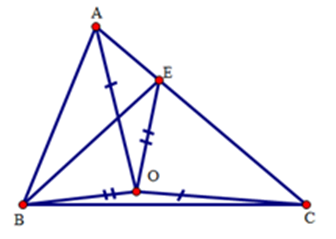
Xét tam giác $AOB$ và tam giác $COE$ có:
$AB = CE\,\left( {gt} \right);AO = CO\,(gt);OB = OE\,(gt)$
Do đó: \(\Delta AOB = \Delta COE(c.c.c)\) suy ra \(\widehat {AOB} = \widehat {COE};\,\widehat {ABO} = \widehat {OEC}\) (hai góc tương ứng bằng nhau)
Nên A, C, D sai, B đúng.
Đáp án : B
Các bài tập cùng chuyên đề
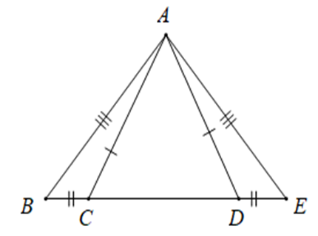
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai:
Cho hình dưới đây.
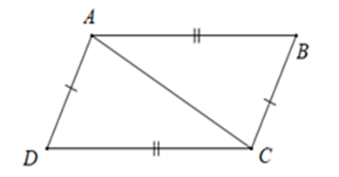
Chọn câu sai.
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
Cho tam giác $ABC$ có $AB = AC$ và $MB = MC$ (\(M \in BC\)). Chọn câu sai.
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm $O$ bán kính bằng $2cm,$ cung tròn này cắt $Ox, Oy$ lần lượt ở $A$ và $B.$ Vẽ các cung tròn tâm $A$ và tâm $B$ có bán kính $3cm,$ chúng cắt nhau tại điểm $C$ nằm trong góc $xOy.$ Tính \(\widehat {xOC}\) .
