Đề bài

Cho tam giác $ABC$ có $AB = AC$ và  $MB = MC$ (\(M \in BC\)). Chọn câu sai.

• A. $\Delta AMC = \Delta BCM$         
• B. $AM \bot BC$          
• C. \(\widehat {BAM} = \widehat {CAM}\)      
• D. \(\Delta AMB = \Delta AMC\)

Lời giải của GV Loigiaihay.com

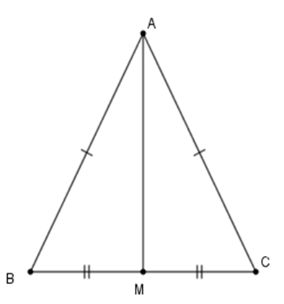
Xét \(\Delta AMB\) và \(\Delta AMC\) có

\(AB = AC\,\left( {gt} \right)\)

\(MB = MC\left( {gt} \right)\)

Cạnh \(AM\) chung

Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)

Suy ra \(\widehat {BAM} = \widehat {CAM}\) và $\widehat {AMB} = \widehat {AMC}$ (hai góc tương ứng bằng nhau) mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \)  (hai góc kề bù)

Nên $\widehat {AMB} = \widehat {AMC} = \dfrac{{180^\circ }}{2} = 90^\circ .$  Hay \(AM \bot BC.\)

Vậy B, C, D đúng, A sai.

Đáp án : A