Cho tam giác ABC có ˆB=800,3ˆA=2ˆC.Tính ˆA và ˆC?
-
A.
ˆA=60∘;ˆC=40∘.
-
B.
ˆA=30∘;ˆC=50∘.
-
C.
ˆA=40∘;ˆC=60∘.
-
D.
ˆA=40∘;ˆC=30∘.
+ Sử dụng định lý tổng ba góc trong tam giác.
+ Sử dụng tính chất dãy tỉ số bằng nhau: ab=cd=a+cb+d.
Xét tam giác ABC có ˆB=800. Theo định lý về tổng ba góc trong tam giác ta có
ˆA+ˆB+ˆC=180∘⇒ˆA+ˆC=180∘−ˆB⇒ˆA+ˆC=100∘.
Lại có 3ˆA=2ˆC⇒ˆA2=ˆC3
Áp dụng tính chất dãy tỉ số bằng nhau ta được
ˆA2=ˆC3=ˆA+ˆC2+3=100∘5=20∘
Suy ra ˆA=40∘;ˆC=60∘.
Đáp án : C

Các bài tập cùng chuyên đề
Tổng ba góc của một tam giác bằng
Cho tam giác ABC vuông tại A. Khi đó
Cho tam giác ABC có ˆA=960,ˆC=500. Số đo góc B là:
Cho hình vẽ sau. Tính số đo x.
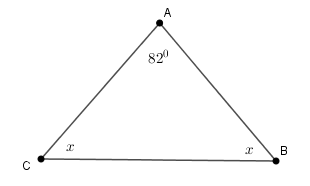
Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc .
Cho hình sau. Tính số đo x.
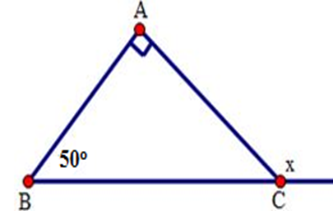
Cho tam giác ABC biết rằng số đo các góc ˆA;ˆB;ˆC tỉ lệ với 2;3;4. Tính ˆB.
Tam giác ABC có ˆA=1000,ˆB−ˆC=400. Số đo góc B và góc C lần lượt là:
Cho tam giác ABC có ˆA=500,ˆB=700. Tia phân giác của góc C cắt cạnh AB tại M. Tính ^AMC và ^BMC.
Cho hình vẽ sau. Tính số đo góc x?
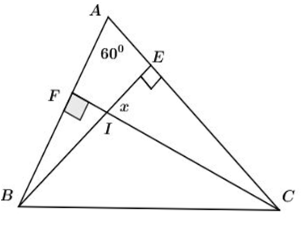
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo ^ADC biết rằng: ˆB−ˆC=200.

















