Cho hình vẽ sau biết $AD//BC.$ Tính \(\widehat {AGB}.\)
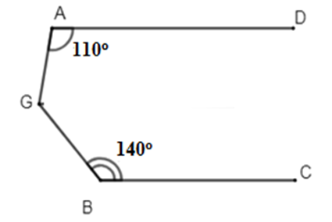
-
A.
\({110^0}\)
-
B.
\({140^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
+ Áp dụng tính chất hai đường thẳng song song.
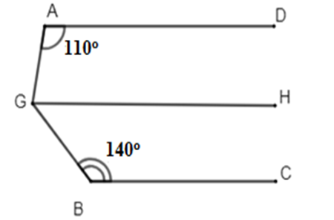
Qua \(G\) kẻ \(GH//AD.\)
Vì \(A{\rm{D}}//\,GH \Rightarrow \widehat {GA{\rm{D}}} + \widehat {AGH} = {180^0} \Rightarrow \widehat {AGH} = {180^0} - \widehat {GA{\rm{D}}} = {180^0} - {110^0} = {70^0}\) (2 góc trong cùng phía bù nhau)
Ta có: \(\left\{ \begin{array}{l}A{\rm{D}}//\,GH\\A{\rm{D}}//\,BC\end{array} \right.\left( {gt} \right) \Rightarrow GH//\,BC\)
\( \Rightarrow \widehat {HGB} + \widehat {GBC} = {180^0} \Rightarrow \widehat {HGB} = {180^0} - \widehat {GBC} = {180^0} - {140^0} = {40^0}\) (2 góc trong cùng phía bù nhau)
\(\widehat {AGB} = \widehat {AGH} + \widehat {HGB} = {70^0} + {40^0} = {110^0}\)
Đáp án : A

Các bài tập cùng chuyên đề
Cho ba đường thẳng phân biệt \(a,\,b\) và c, biết \(a//b\) và \(a \bot c\). Kết luận nào đúng:
Cho ba đường thẳng phân biệt a, b, c, biết \(a//b\) và \(b//c\) . Chọn kết luận đúng:
Cho hình vẽ sau:
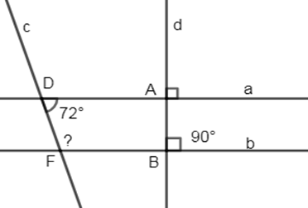
Biết \(a \bot d,\,b \bot d,\,\widehat {A{\rm{D}}F} = {72^0}\). Tính \(\widehat {DFB}\).
Cho hai đường thẳng $a$ và $b$ cùng vuông góc với đường thẳng $c,$ $c$ vuông góc với $a$ tại $M$ và vuông góc với $b$ tại $N.$ Một đường thẳng $m$ cắt $a,b$ tại $A,B.$ Biết \(\widehat {ABN} - \widehat {MAB} = 40^\circ \). Số đo góc $BAM$ là:
Cho hình vẽ sau:
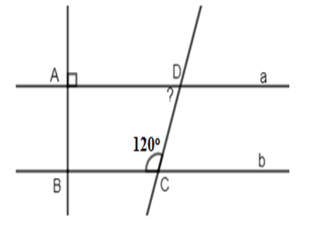
Biết \(a//\,b,\,\widehat {BC{\rm{D}}} = {120^0}\) và $a \bot AB$. Kết luận nào sau đây là đúng:
Cho hình vẽ sau:
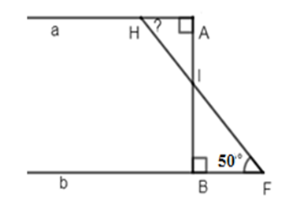
Biết \(AB \bot a,\,AB \bot b,\,\widehat {BFH} = {50^0}\). Tính \(\widehat {AHF}\).
Cho hình vẽ sau. Tính số đo góc \(BAD.\)
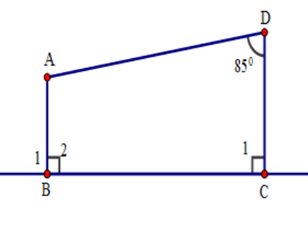
Cho hình vẽ sau:
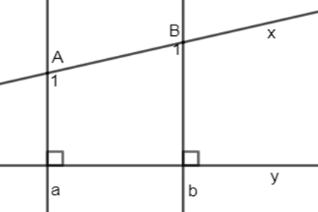
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\). Tính \(\widehat {{B_1}}\).
Cho hình vẽ sau:
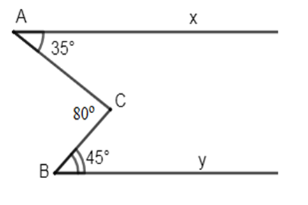
Biết \(\widehat {xAC} = {35^0},\,\widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Khi đó chọn câu đúng.
Cho hình vẽ sau
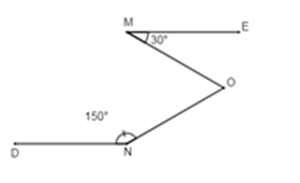
Biết \(ME//N{\rm{D}},\,\widehat {EM{\rm{O}}} = {30^0},\,\widehat {DNO} = {150^0}\). Tính \(\widehat {MON}\) .

















