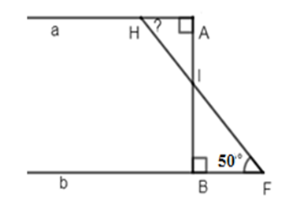
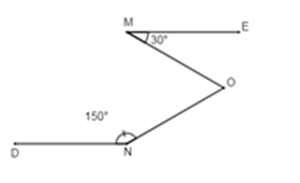
Cho hình vẽ sau. Tính số đo góc
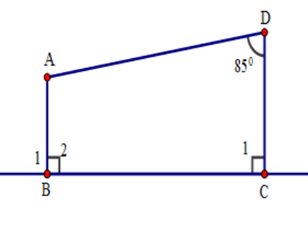
-
A.
-
B.
-
C.
-
D.
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
+ Tính chất hai đường thẳng song song.
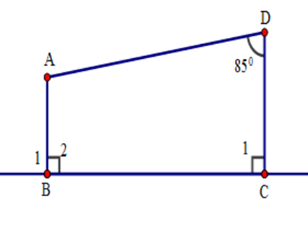
Ta thấy (quan hệ từ vuông góc đến song song)
Suy ra (hai góc trong cùng phía bù nhau)
Vậy
Đáp án : A

Các bài tập cùng chuyên đề
Cho ba đường thẳng phân biệt và c, biết và . Kết luận nào đúng:
Cho ba đường thẳng phân biệt a, b, c, biết và . Chọn kết luận đúng:
Cho hình vẽ sau:
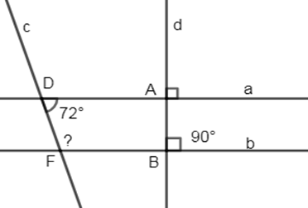
Biết . Tính .
Cho hai đường thẳng và cùng vuông góc với đường thẳng vuông góc với tại và vuông góc với tại Một đường thẳng cắt tại Biết . Số đo góc là:
Cho hình vẽ sau:
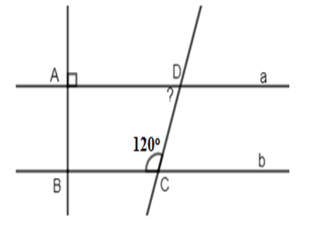
Biết và . Kết luận nào sau đây là đúng:
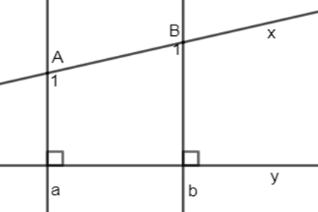
Cho hình vẽ sau:
Biết . Tính .
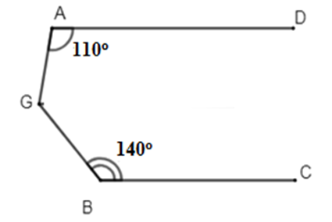
Cho hình vẽ sau:
Biết . Tính .
Cho hình vẽ sau biết Tính
Cho hình vẽ sau:
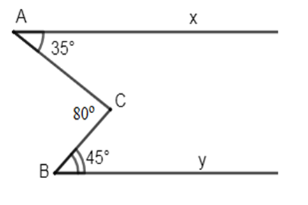
Biết và Khi đó chọn câu đúng.
Cho hình vẽ sau
Biết . Tính .

















