Đề bài
Vẽ \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
-
A.
$124^\circ$
-
B.
$142^\circ$
-
C.
$65^\circ$
-
D.
$56^\circ$
Phương pháp giải
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
Lời giải của GV Loigiaihay.com
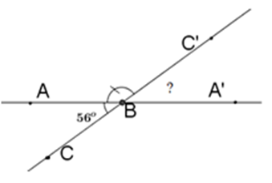
Vì góc \(ABC'\) kề bù với góc $ABC$ nên $BC'$ là tia đối của tia $BC.$
Vì góc $C'BA'$ kề bù với góc $ABC'$ nên $BA'$ là tia đối của tia $BA.$
Do đó, góc $C'BA'$ và góc $ABC$ đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Đáp án : D

Các bài tập cùng chuyên đề


















Danh sách bình luận