Đề bài

Số ${x^{12}}$ (với $x \ne 0$) không bằng số nào trong các số sau đây ?

A.

${x^{18}}:{x^6}(x\; \ne 0)$
B.

${x^4}.{\rm{ }}{x^8}$
C.

${x^2}.{\rm{ }}{x^6}$
D.

${\left( {{x^3}} \right)^4}$

Phương pháp giải

Ta áp dụng các công thức sau: ${x^m}.{x^n} = {x^{m + n}};{x^m}:{x^n} = {x^{m - n}}$$\left( {m \ge n,x \ne 0;m,n \in {N^ * }} \right)$, ${\left( {{x^m}} \right)^n} = {x^{m.n}}$

Lời giải của GV Loigiaihay.com

Ta có

+) ${x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}(x\; \ne 0)$ nên A đúng.

+) ${x^4}.{\rm{ }}{x^8} = {x^{4 + 8}} = {x^{12}}$ nên B đúng.

+ ${\left( {{x^3}} \right)^4} = {x^{3.4}} = {x^{12}}$ nên D đúng.

Ta thấy ở đáp án C: ${x^2}.{x^6} = {x^{2 + 6}} = {x^8} \ne {x^{12}}$

nên C sai.

Đáp án : C

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Số ${x^4}$ không bằng số nào trong các số sau đây?

A.

${x^{12}}:{x^8}\,(x \ne 0)$
B.

${x^2}.{x^3}$
C.

${\left( {{x^2}} \right)^2}$
D.

${x^5}:x\, (x \ne 0)$

Xem lời giải >>

Bài 2 :

Số ${x^{18}}$ (với $x \ne 0$) bằng số nào trong các số sau đây ?

A.
${x^{12}}:{x^6}\left( {x \ne 0} \right)$
B.
${\left( {{x^{12}}} \right)^6}$
C.
${\left( {{x^2}} \right)^9}$
D.
${x^3}.{x^6}$

Xem lời giải >>

Bài 3 :

Số ${x^{9}}$ bằng số nào trong các số sau đây ?

A.
${x^{18}}:{x^2}\left( {x \ne 0} \right)$
B.
${\left( {{x^3}} \right)^6}$
C.
${\left( {{x^2}} \right)^7}$
D.
${x^3}.{x^6}$

Xem lời giải >>

Bài 4 :

Số ${x^{10}}$ bằng số nào trong các số sau đây ?

A.
${x^{15}}:{x^5}\left( {x \ne 0} \right)$
B.
${\left( {{x^3}} \right)^7}$
C.
${\left( {{x^8}} \right)^2}$
D.
${\left( {{x^8}} \right)^2}$

Xem lời giải >>

Bài 5 :

Tính và so sánh:

a) ${( - 3)^2}.{( - 3)^4}$ và ${( - 3)^6}$;

b) $0,6{}^3:0,{6^2}$ và $0,{6}$

Xem lời giải >>

Bài 6 :

Viết kết quả của các phép tính sau dưới dạng lũy thừa.

$\begin{array}{l}a){( - 2)^3}.{( - 2)^4};\\b){(0,25)^7}:{(0,25)^3}\end{array}$

Xem lời giải >>

Bài 7 :

Thay mỗi dấu “?” bởi một lũy thừa của 3, biết rằng từ ô thứ ba, lũy thừa cần tìm là tích của hai lũy thừa ở hai ô liền trước.

Xem lời giải >>

Bài 8 :

Không sử dụng máy tính, hãy tính:

a) ${( - 3)^8}$ biết ${( - 3)^7} = - 2187$

b) ${\left( { - \frac{2}{3}} \right)^{12}}$ biết ${\left( { - \frac{2}{3}} \right)^{11}} = \frac{{ - 2048}}{{177147}}$

Xem lời giải >>

Bài 9 :

Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ.

$\begin{array}{l}a){15^8}{.2^4};\\b){27^5}:{32^3}\end{array}$

Xem lời giải >>

Bài 10 :

Khoảng cách từ Trái Đất đến Mặt Trời bằng khoảng $1,{5.10^8}$ km. Khoảng cách từ Mộc tinh đến Mặt Trời khoảng $7,{78.10^8}$ km. Hỏi khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng bao nhiêu lần khoảng cách từ Trái Đất đến Mặt Trời?

(Theo solarsystem.nasa.gov)

Xem lời giải >>

Bài 11 :

Tìm số thích hợp thay vào dấu “?” trong các câu dưới đây:

a)${\left( {\frac{1}{3}} \right)^2}.{\left( {\frac{1}{3}} \right)^2} = {\left( {\frac{1}{3}} \right)^?}$ b)${\left( {0,2} \right)^2}.{\left( {0,2} \right)^3} = {\left( {0,2} \right)^?}$.

Xem lời giải >>

Bài 12 :

Tính:

a)${\left( { - 2} \right)^2}.{\left( { - 2} \right)^3}$;

b)${\left( { - 0,25} \right)^7}:{\left( { - 0,25} \right)^5}$;

c)${\left( {\frac{3}{4}} \right)^4}.{\left( {\frac{3}{4}} \right)^3}.$

Xem lời giải >>

Bài 13 :

Tìm x, biết:

a)$x:{\left( {\frac{{ - 1}}{2}} \right)^3} = - \frac{1}{2};$ b)$x.{\left( {\frac{3}{5}} \right)^7} = {\left( {\frac{3}{5}} \right)^9};$

c)${\left( {\frac{{ - 2}}{3}} \right)^{11}}:x = {\left( {\frac{{ - 2}}{3}} \right)^9};$ d)$x.{\left( {0,25} \right)^6} = {\left( {\frac{1}{4}} \right)^8}$

Xem lời giải >>

Bài 14 :

Tính:

a)$\left[ {{{\left( {\frac{3}{7}} \right)}^4}.{{\left( {\frac{3}{7}} \right)}^5}} \right]:{\left( {\frac{3}{7}} \right)^7};$

b)$\left[ {{{\left( {\frac{7}{8}} \right)}^5}:{{\left( {\frac{7}{8}} \right)}^4}} \right].\left( {\frac{7}{8}} \right);$

c)$\left[ {{{\left( {0,6} \right)}^3}.{{\left( {0,6} \right)}^8}} \right]:\left[ {{{\left( {0,6} \right)}^7}.{{\left( {0,6} \right)}^2}} \right]$.

Xem lời giải >>

Bài 15 :

a) Khối lượng của Trái Đất khoảng 5,97.10²⁴ kg, khối lượng của Mặt Trăng khoảng 7,35.10²² kg. Tính tổng khối lượng của Trái Đất và Mặt Trăng.

b) Sao Mộc cách Trái Đất khoảng 8,27.10⁸ km, Sao Thiên Vương cách Trái Đất khoảng 3,09.10⁹ km. Sao nào ở gần Trái Đất hơn?

(Theo: https://vi.wikipedia.org/wiki/Hệ Mặt Trời)

Xem lời giải >>

Bài 16 :

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

a) ${2^m}{.2^n}$

b) ${3^m}:{3^n}$ với $m \ge n$

Xem lời giải >>

Bài 17 :

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

a)$\frac{6}{5}.{\left( {1,2} \right)^8};$

b)${\left( {\frac{{ - 4}}{9}} \right)^7}:\frac{{16}}{{81}}$

Xem lời giải >>

Bài 18 :

So sánh:

a) ${( - 2)^4} \cdot {( - 2)^5}$ và ${( - 2)^{12}}:{( - 2)^3}$;

b) ${\left( {\frac{1}{2}} \right)^2} \cdot {\left( {\frac{1}{2}} \right)^6}$ và ${\left[ {{{\left( {\frac{1}{2}} \right)}^4}} \right]^2}$

c) ${(0,3)^8}:{(0,3)^2}$ và ${\left[ {{{(0,3)}^2}} \right]^3}$;

d) ${\left( { - \frac{3}{2}} \right)^5}:{\left( { - \frac{3}{2}} \right)^3}$ và ${\left( {\frac{3}{2}} \right)^2}$.

Xem lời giải >>

Bài 19 :

Tìm x, biết:

a) ${(1,2)^3}.x = {(1,2)^5};$

b) ${\left( {\frac{2}{3}} \right)^7}:x = {\left( {\frac{2}{3}} \right)^6}$

Xem lời giải >>

Bài 20 :

Viết kết quả mỗi phép tính sau dưới dạng luỹ thừa của $a$ :

a) ${\left( {\frac{8}{9}} \right)^3} \cdot \frac{4}{3} \cdot \frac{2}{3}$ với $a = \frac{8}{9};$

b) ${\left( {\frac{1}{4}} \right)^7} \cdot 0,25$ với $a = 0,25$;

c) ${( - 0,125)^6}:\frac{{ - 1}}{8}$ với $a = - \frac{1}{8};$

d) ${\left[ {{{\left( {\frac{{ - 3}}{2}} \right)}^3}} \right]^2}$ với $a = \frac{{ - 3}}{2}$.

Xem lời giải >>

Bài 21 :

Viết các số sau dưới dạng luỹ thừa của một số hữu tỉ.

a) $125.27$

b) $243:32$

Xem lời giải >>

Bài 22 :

Tính giá trị của biểu thức:

a)${\left( {\dfrac{1}{2}} \right)^3}.4 + \dfrac{3}{4}$

b)${4^3}:{2^5} + {3^5}:{9^2}$

Xem lời giải >>

Bài 23 :

Bảng thống kê dưới đây ước lượng số dân của một số nước tại thời điểm năm 2020.

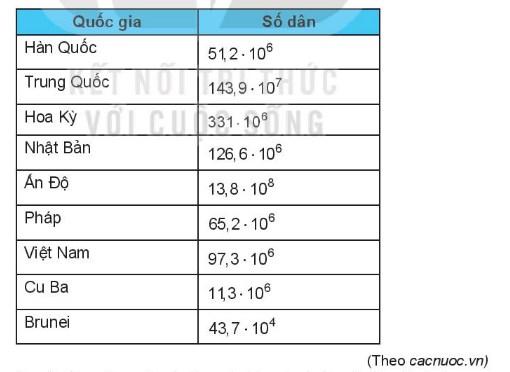
Em hãy sắp xếp tên các quốc gia theo thứ tự có số dân từ lớn đến bé.

Xem lời giải >>

Bài 24 :

Thay dấu “?” bằng số thích hợp:

a)${\left( {\dfrac{2}{3}} \right)^5}.{\left( {\dfrac{2}{3}} \right)^?} = {\left( {\dfrac{2}{3}} \right)^8};$

b)${\left( { - \dfrac{3}{4}} \right)^?}:{\left( {\dfrac{{ - 3}}{4}} \right)^7} = {\left( {\dfrac{{ - 3}}{4}} \right)^2}$

Xem lời giải >>

Bài 25 :

Không sử dụng máy tính cầm tay, hãy tính:

a)${\left( { - 5} \right)^7}$, biết ${\left( { - 5} \right)^6} = 15625$

b) ${2^{12}}$ , biết ${2^{11}} = 2048$

Xem lời giải >>

Bài 26 :

Hình vuông dưới đây có tính chất: Mỗi ô ghi một luỹ thừa của 2; tích các số trong mỗi hàng, mỗi cột, mỗi đường chéo đều bằng nhau. Hãy điền các luỹ thừa của 2 còn thiếu vào các ô trống:

Xem lời giải >>

Bài 27 :

Tính

a) ${\left( {\dfrac{{ - 2}}{3}} \right)^3}.{\left( {\dfrac{{ - 2}}{3}} \right)^2}$

b) ${(0,15)^7}:{(0,15)^5}$

c) ${\left( {\dfrac{3}{5}} \right)^{15}}:{\left( {\dfrac{{27}}{{125}}} \right)^5}$

d) ${\left( {\dfrac{1}{7}} \right)^4}.\dfrac{1}{7}{.49^3}$

Xem lời giải >>

Bài 28 :

Tìm x, biết:

a) $x:{\left( {\dfrac{{ - 1}}{3}} \right)^3} = \dfrac{{ - 1}}{3}$

b) $x.{\left( {\dfrac{{ - 3}}{7}} \right)^5} = {\left( {\dfrac{{ - 3}}{7}} \right)^7}$

c) ${\left( {\dfrac{{ - 2}}{3}} \right)^{12}}:x = {\left( {\dfrac{{ - 2}}{3}} \right)^9}$

d) ${\left( {x + \dfrac{1}{3}} \right)^2} = \dfrac{1}{{25}}$

Xem lời giải >>

Bài 29 :

Tính

a) $\left[ {{{\left( {\dfrac{2}{5}} \right)}^6}.{{\left( {\dfrac{2}{5}} \right)}^5}} \right]:{\left( {\dfrac{2}{5}} \right)^9}$

b) $\left[ {{{\left( {\dfrac{3}{7}} \right)}^8}:{{\left( {\dfrac{3}{7}} \right)}^7}} \right].\left( {\dfrac{3}{7}} \right)$

c) $\left[ {{{\left( {\dfrac{2}{5}} \right)}^9}.{{\left( {\dfrac{2}{5}} \right)}^4}} \right]:\left[ {{{\left( {\dfrac{2}{5}} \right)}^7}.{{\left( {\dfrac{2}{5}} \right)}^3}} \right]$

Xem lời giải >>

Bài 30 :

So sánh:

a) ${\left( { - {\rm{ }}0,1} \right)^2}.{\left( { - {\rm{ }}0,1} \right)^4}$ và ${\left[ {{{\left( { - {\rm{ }}0,1} \right)}^3}} \right]^2}$;

b) ${\left( {\dfrac{1}{2}} \right)^8}:{\left( {\dfrac{1}{2}} \right)^2}$ và ${\left( {\dfrac{1}{2}} \right)^3}.{\left( {\dfrac{1}{2}} \right)^3}$;

c) ${9^8}:{27^3}$ và ${3^2}{.3^5}$;

d) ${\left( {\dfrac{1}{4}} \right)^7}.0,25$ và ${\left[ {{{\left( {\dfrac{1}{4}} \right)}^2}} \right]^4}$;

e) ${\left[ {{{\left( { - {\rm{ }}0,7} \right)}^2}} \right]^3}$ và ${\left[ {{{\left( {0,7} \right)}^3}} \right]^2}$.

Xem lời giải >>