Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
-
A.
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
-
B.
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
-
C.
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
-
D.
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
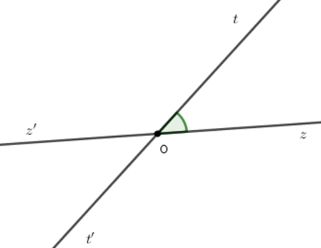
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\)
Thay \(\widehat {tOz'} = 4.\widehat {tOz}\), ta được:
\(\widehat {zOt} + 4.\widehat {zOt} = 180^\circ \)
\(5.\widehat {zOt} = 180^\circ \)
\(\widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Đáp án : C

Các bài tập cùng chuyên đề

















