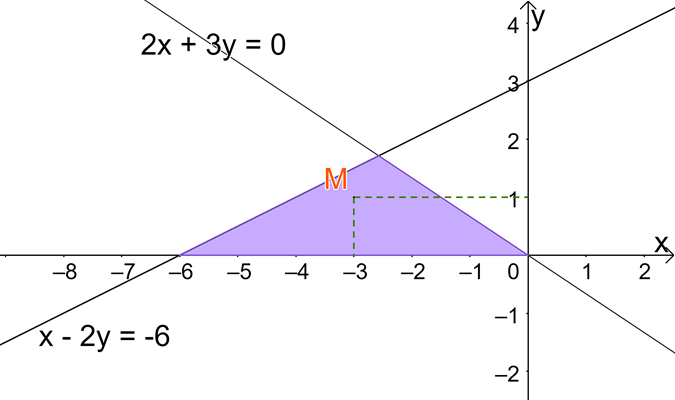
Phần tô màu trong hình dưới đây biểu diễn miền nghiệm của hệ bất phương trình nào?
-
A.
\(\left\{ \begin{array}{l}x - 2y + 6 \le 0\\2x - 3y \ge 0\\x \ge 0\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x - 2y + 6 \ge 0\\2x - 3y \le 0\\x \ge 0\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x - 2y + 6 \ge 0\\2x - 3y \ge 0\\x \le 0\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x - 2y + 6 \ge 0\\2x - 3y \le 0\\x \le 0\end{array} \right.\)
Thay tọa độ điểm M vào mỗi BPT, loại dần các đáp án.
+) Điểm \(M( - 3;1)\) thuộc miền nghiệm, đo đó:
Đáp án A, B. Loại vì \(x = - 3 < 0\)
Đáp án C Loại vì \(2.( - 3) - 3.1 = - 9 < 0\)
Đáp án D thỏa mãn vì \(\left\{ \begin{array}{l} - 3 - 2.1 + 6 = 1 \ge 0\\2.( - 3) - 3.1 = - 9 < 0\\ - 3 < 0\end{array} \right.\)
Đáp án : D
Các bài tập cùng chuyên đề
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Cặp số nào sau đây là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}3x - 5y > 12\\x - 2y \le 7\end{array} \right.\)
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + 2(y + 1) - 4y \le 2(x + 1) - 5y\\x + y \ge 0\end{array} \right.\) không chứa điểm có tọa độ:
Điểm \(A(1;2)\) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\2x + 3y > 6\end{array} \right.\) là phần không gạch trong hình nào dưới đây?
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y \le 6\\3x - y \le 12\\x \ge 0\\y \ge 0\end{array} \right.\) có miền nghiệm là miền tứ giác OABC như hình dưới. Giá trị lớn nhất của \(F = 28x + 49y\) là:
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + y \le 6\\3x - 4y \le 6\\5x - 2y \ge 0\\x \le 2\\y \ge - 1\end{array} \right.\)
có miền nghiệm là miền ngũ giác ABCDE như hình dưới. Giá trị nhỏ nhất của \(F = 15x - 9y\) là:
