Đề bài

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + 2(y + 1) - 4y \le 2(x + 1) - 5y\\x + y \ge 0\end{array} \right.\) không chứa điểm có tọa độ:

A.

\((1; - 1)\)
B.

\((1;0)\)
C.

\((3;2)\)
D.

\((10;3)\)

Lời giải của GV Loigiaihay.com

Cả 4 cặp số đều thỏa mãn BPT \(x + y \ge 0\), nên ta kiểm tra với BPT còn lại:

\(x + 2(y + 1) - 4y \le 2(x + 1) - 5y\)

\(\Leftrightarrow x + 2y + 2 - 4y - (2x + 2 - 5y) \le 0\)

\(\Leftrightarrow - x + 3y \le 0\).

Vì \( - 3 + 3.2 = 3 > 0\) nên (3; 2) không là nghiệm của một BPT trong hệ.

Vậy (3; 2) không là nghiệm của hệ BPT đã cho.

Đáp án : C

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

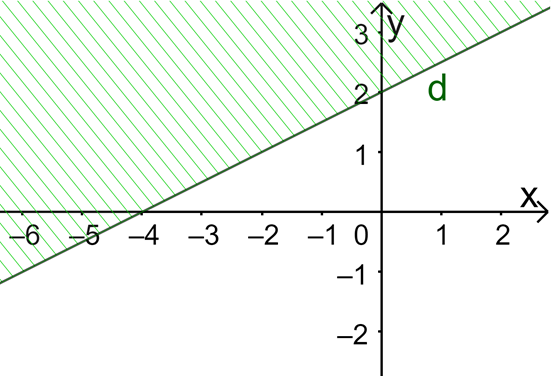
Phần không gạch chéo (không kể bờ d) trong hình dưới đây biểu diễn miền nghiệm của bất phương trình nào?

A.

\(x - 2y + 4 > 0\)
B.

\(x - 2y + 4 \ge 0\)
C.

\(x + 2y < 2\)
D.

\(x + 2y \le 2\)

Xem lời giải >>

Bài 2 :

Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ: \(\left\{ \begin{array}{l}x \ge 0\\y > 0\\x + y \le 100\\2x + y < 120\end{array} \right.\)

Xem lời giải >>

Bài 3 :

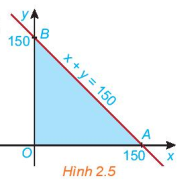
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.

a) Xác định miền nghiệm \({D_1},{D_2},{D_3}\) của các bất phương trình tương ứng \(x \ge 0;y \ge 0\) và \(x + y \le 150\).

b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\) hay không?

c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:

\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Xem lời giải >>

Bài 4 :

c) \(\left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y > 0\end{array} \right.\)

Xem lời giải >>

Bài 5 :

b) \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.\)

Xem lời giải >>

Bài 6 :

a) \(\left\{ \begin{array}{l}y - x < - 1\\x > 0\\y < 0\end{array} \right.\)

Xem lời giải >>

Bài 7 :

Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < - 3\\2y \ge - 4\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?

A. (0;0)

B. (-2;1)

C. (3;-1)

D. (-3;1)

Xem lời giải >>

Bài 8 :

Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y < 1\\2x - y \ge 3\end{array} \right.\) trên mặt phẳng tọa độ

Xem lời giải >>

Bài 9 :

Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\y \le 4\\x \le 5\\x + y \ge - 1\end{array} \right.\) trên mặt phẳng tọa độ.

Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x - y\) với \(\left( {x;y} \right)\) thỏa mãn hệ trên.

Xem lời giải >>

Bài 10 :

Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x - y > - 3\\ - 2x + 3y < 6\\2x + y > - 4\end{array} \right.\).

Xem lời giải >>

Bài 11 :

Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x - 2y \ge - 2\\7x - 4y \le 16\\2x + y \ge - 4\end{array} \right.\)

a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình

trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

b) Tìm miền nghiệm của hệ bất phương trình đã cho.

Xem lời giải >>

Bài 12 :

Biểu diễn miền nghiệm của hệ bất phương trình:

a) \(\left\{ \begin{array}{l}x + 2y < - 4\\y \ge x + 5\end{array} \right.\)

b) \(\left\{ \begin{array}{l}4x - 2y > 8\\x \ge 0\\y \le 0\end{array} \right.\)

Xem lời giải >>

Bài 13 :

Biểu diễn miền nghiệm của hệ bất phương trình:

a) \(\left\{ \begin{array}{l}2x - 3y < 6\\2x + y < 2\end{array} \right.\)

b) \(\left\{ \begin{array}{l}4x + 10y \le 20\\x - y \le 4\\x \ge - 2\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x - 2y \le 5\\x + y \ge 2\\x \ge 0\\y \le 3\end{array} \right.\)

Xem lời giải >>

Bài 14 :

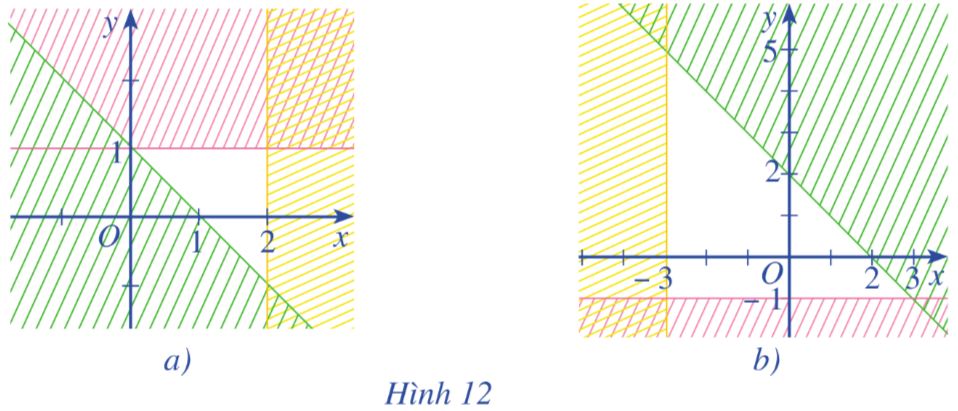
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

a) \(\left\{ \begin{array}{l}x + y \le 2\\x \ge - 3\\y \ge - 1\end{array} \right.\)

b) \(\left\{ \begin{array}{l}y \le x\\x \le 0\\y \ge - 3\end{array} \right.\)

c) \(\left\{ \begin{array}{l}y \ge - x + 1\\x \le 2\\y \le 1\end{array} \right.\)

Xem lời giải >>

Bài 15 :

Biểu diễn miền nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \le 8\\2x + 3y \le 18\\x \ge 0\\y \ge 0\end{array} \right.\)

Xem lời giải >>

Bài 16 :

Cho hệ bất phương trình: \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\end{array} \right.\)

Miền nào trong Hình 1 biểu diễn phần giao các miền nghiệm của hai bất phương trình trong hệ đã cho?

Xem lời giải >>

Bài 17 :

Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:

a) \(\left\{ \begin{array}{l}x + y - 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x \ge 1\\x \le 4\\x + y - 5 \le 0\\y \ge 0\end{array} \right.\)

Xem lời giải >>

Bài 18 :

Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ Oxy: \(\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < 3\end{array} \right.\).

Xem lời giải >>

Bài 19 :

Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 3y - 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?

A.

M(0;1)
B.

N(-1;1)
C.

P(1;3)
D.

Q(-1;0)

Xem lời giải >>

Bài 20 :

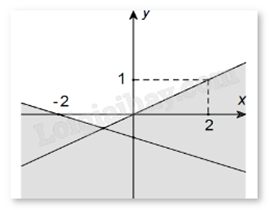
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

A.

\(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \ge - 2}\end{array}} \right.\)
B.

\(\left\{ {\begin{array}{*{20}{c}}{x - 2y > 0}\\{x + 3y < - 2}\end{array}} \right.\)
C.

\(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \le - 2}\end{array}} \right.\)
D.

\(\left\{ {\begin{array}{*{20}{c}}{x - 2y < 0}\\{x + 3y > - 2}\end{array}} \right.\)

Xem lời giải >>

Bài 21 :

Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + y \ge 9}\\{x \ge y - 3}\\{2y \ge 8 - x}\\{y \le 6}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?

A.

O(0;0)
B.

M(1;2)
C.

N(2;1)
D.

P(8;4)

Xem lời giải >>

Bài 22 :

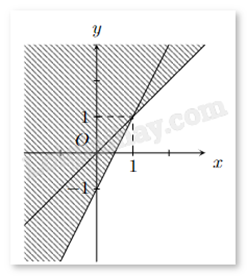
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

A.

\(\left\{ {\begin{array}{*{20}{c}}{x - y \ge 0}\\{2x - y \ge 1}\end{array}} \right.\)
B.

\(\left\{ {\begin{array}{*{20}{c}}{x - y > 0}\\{2x - y > 1}\end{array}} \right.\)
C.

\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y > 1}\end{array}} \right.\)
D.

\(\left\{ {\begin{array}{*{20}{c}}{x - y < 0}\\{2x - y < 1}\end{array}} \right.\)

Xem lời giải >>

Bài 23 :

Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\) chứa điểm nào trong các điểm sau đây?

A.

\((0;0)\)
B.

\((1;0)\)
C.

\((0; - 2)\)
D.

\((0;2)\)

Xem lời giải >>

Bài 24 :

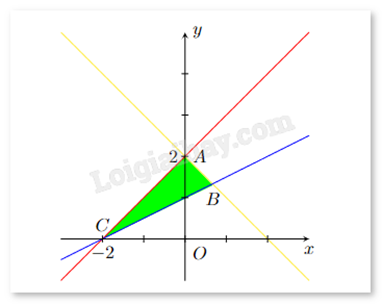
Miền tam giác (kể cả ba cạnh AB, BC, CA) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

A.

\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
B.

\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \ge 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
C.

\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \le 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
D.

\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \ge 0}\end{array}} \right.\)

Xem lời giải >>

Bài 25 :

Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:

a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)

b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x - y - 4 < 0}\end{array}} \right.\)

c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge - 1}\\{y \ge - 2}\end{array}} \right.\)

Xem lời giải >>

Bài 26 :

Điểm nào sau đây thuộc miền nghiệm của bất phương trình \(2x + 5y \le 10?\)

A. \(\left( {5;2} \right).\)

B. \(\left( { - 1;4} \right).\)

C. \(\left( {2;1} \right).\)

D. \(\left( { - 5;6} \right).\)

Xem lời giải >>

Bài 27 :

Cặp số nào dưới đây là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 2}\\{x - 2y \ge 4}\\{x > 0}\end{array}\,\,?} \right.\)

A. \(\left( { - 1;2} \right).\)

B. \(\left( { - 2; - 4} \right).\)

C. \(\left( {0;1} \right).\)

D. \(\left( {2;4} \right).\)

Xem lời giải >>

Bài 28 :

Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - x + y \le 2}\\{x - 2y \ge 1}\\{y \le 0}\end{array}\,\,?} \right.\)

A. \(\left( { - 3;2} \right).\)

B. \(\left( {0;1} \right).\)

C. \(\left( {4; - 1} \right).\)

D. \(\left( { - 2;2} \right).\)

Xem lời giải >>

Bài 29 :

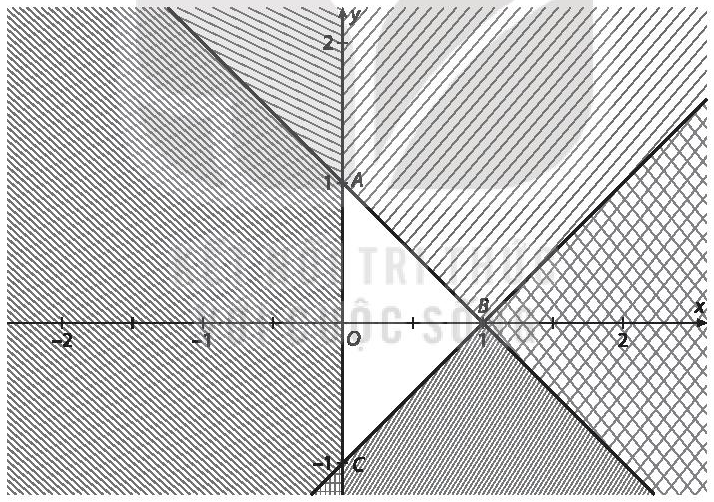
Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác \(ABC\) (miền không bị gạch)?

A. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \ge 1}\\{x \ge 0}\end{array}.} \right.\)

B. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right..\)

C. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{x \ge 0}\end{array}.} \right.\)

D. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{y \ge 0}\end{array}.} \right.\)

Xem lời giải >>

Bài 30 :

Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{x + y \le 0}\\{y \ge 0}\end{array}} \right.\) là:

A. Một nửa mặt phẳng.

B. Miền tam giác.

C. Miền tứ giác.

D. Miền ngũ giác.

Xem lời giải >>