Tìm số hữu tỉ x biết rằng \(\dfrac{x}{{{y^2}}} = 2\) và \(\dfrac{x}{y} = 16\) \(\left( {y \ne 0} \right).\)
-
A.
\(x = 16\)
-
B.
\(x = 128\)
-
C.
\(x = 8\)
-
D.
\(x = 256\)
Từ giả thiết biến đổi để tìm được \(y\), từ đó thay \(y\) vào \(\dfrac{x}{y} = 16\) để tìm \(x\)
Ta có \(\dfrac{x}{{{y^2}}} = 2\) nên \(\dfrac{x}{y}.\dfrac{1}{y} = 2\), mà \(\dfrac{x}{y} = 16\). Do đó:
\(16.\dfrac{1}{y} = 2\)
\(\dfrac{1}{y} = \dfrac{1}{8}\)
\(y = 8\)
Thay \(y = 8\) vào \(\dfrac{x}{y} = 16\) ta được: \(\dfrac{x}{8} = 16\) nên \(x = 16.8 = 128\).
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Chỉ ra đáp án sai: Từ tỉ lệ thức \(\dfrac{5}{9} = \dfrac{{35}}{{63}}\) ta có tỉ lệ thức sau:
-
A.
\(\dfrac{5}{{35}} = \dfrac{9}{{63}}\)
-
B.
\(\dfrac{{63}}{9} = \dfrac{{35}}{5}\)
-
C.
\(\dfrac{{35}}{9} = \dfrac{{63}}{5}\)
-
D.
\(\dfrac{{63}}{{35}} = \dfrac{9}{5}\)
Bài 2 :
Các tỉ số nào sau đây lập thành một tỉ lệ thức?
-
A.
\(\dfrac{7}{{12}}\) và \(\dfrac{5}{6}:\dfrac{4}{3}\)
-
B.
\(\dfrac{6}{7}:\dfrac{{14}}{5}\) và \(\dfrac{7}{3}:\dfrac{2}{9}\)
-
C.
\(\dfrac{{15}}{{21}}\) và \( - \dfrac{{125}}{{175}}\)
-
D.
\(\dfrac{{ - 1}}{3}\) và \(\dfrac{{ - 19}}{{57}}\)
Bài 3 :
Có hai thanh sắt phi 18: thanh thứ nhất dài 2 m có khối lượng là 4 kg; thanh thứ hai dài 5 m có khối lượng là 10 kg.
Em có nhận xét gì về tỉ số giữa khối lượng của thanh sắt thứ nhất và khối lượng của thanh sắt thứ hai với tỉ số giữa chiều dài của thanh sắt thứ nhất và chiều dài của thanh sắt thứ hai?
Bài 4 :
So sánh hai tỉ số \(\frac{{12}}{{28}}\) và \(\frac{{7,5}}{{17,5}}\)
Bài 5 :
Từ các tỉ số sau đây có lập được tỉ lệ thức không?
a) \(\frac{{ - 2}}{5}:4\) và \(\frac{3}{4}:\frac{{ - 15}}{2}\);
b) \(\frac{{15}}{{27}}\) và 25:30
Bài 6 :
Từ các tỉ số sau đây có lập được tỉ lệ thức không?
a) 3,5 : (-5,25) và (-8) : 12
b) \(39\frac{3}{{10}}:52\frac{2}{5}\) và 7,5 : 10
c) 0,8 : (-0,6) và 1,2 : (-1.8)
Bài 7 :
Lập tất cả các tỉ lệ thức có thể có được từ bốn số sau: 1,5; 2; 3,6; 4,8.
Bài 8 :
Hình 14a mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp đó. Hình 14b mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp khi đặt hộp ngược lại. Tính tỉ số của thể tích sữa có trong hộp và thể tích của cả hộp.
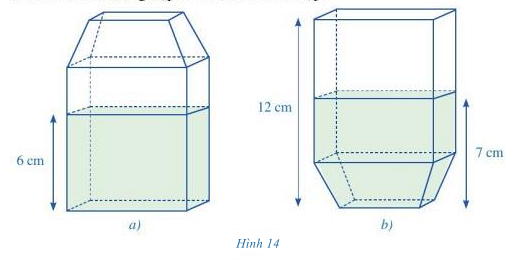
Bài 9 :
Lần thứ nhất bác Dũng xay 100 kg thóc được 65 kg gạo. Lần thứ hai bác xay 30 kg thóc được 19,5 kg gạo.
a) Tính tỉ số giữa khối lượng thóc xay lần thứ nhất và khối lượng thóc xay lần thứ hai; tỉ số giữa khối lượng gạo lần thứ nhất và khối lượng gạo lần thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức không?
Bài 10 :
Từ các số sau đây có thể lập được tỉ lệ thức không?
a) \(16:6\) và \(40:15\).
b) \(\dfrac{2}{3}:\dfrac{1}{4}\) và \(12:( - 3)\).
c) \(( - 3,9):2,4\) và \(5,85:( - 3,6)\).
d) \(\sqrt 9 :2\) và \(\sqrt {36} :4\).
Bài 11 :
Thùng thứ nhất chứa 17 l dầu nặng 13,6 kg. Thùng thứ hai chứa 15 l dầu nặng 12 kg.
a) Tính tỉ số giữa thể tích dầu của thùng thứ nhất và thể tích dầu của thùng thứ hai; tỉ số khối lượng dầu của thùng thứ nhất và khối lượng dầu của thùng thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức không?
Bài 12 :
Lập tất cả các tỉ lệ thức có thể có được từ bốn số sau:
a) 12; 21; 84; 3;
b) 0,36; 4,25; 0,9; 1,7;
c) \(\dfrac{3}{5};{\rm{ }}6;{\rm{ }}\dfrac{4}{5};{\rm{ }}8\);
d) \(2,5;{\rm{ }} - 5,12;{\rm{ }} - 3,2;{\rm{ }}4\).
Bài 13 :
Cho 3 số 6, 8, 24.
a) Tìm số x sao cho x cùng với ba số trên lập thành một tỉ lệ thức.
b) Lập tất cả các tỉ lệ thức có thể có được.
Bài 14 :
Tìm \(x\), biết:
a) \({\left( {2x + 1} \right)^2} = 25\)
b) \(\frac{{2 - x}}{4} = \frac{{3x - 1}}{{ - 3}}\)
Bài 15 :
Lá quốc kì cắm trên đỉnh cột cờ Lũng Cú, Hà Giang có chiều rộng 6 m, chiều dài 9 m. Lá quốc kì bố Linh treo tại nhà mỗi dịp lễ có 0,8 m, chiều dài 1,2 m.
a) Tính tỉ số giữa chiều rộng và chiều dài của mỗi lá cờ. Viết kết quả này dưới dạng phân số tối giản.
b) So sánh hai tỉ số nhận được.
Bài 16 :
Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức tương ứng:
\(4:20;0,5:1,25;\frac{3}{5}:\frac{3}{2}\)
Bài 17 :

Hãy giúp bạn Vuông trả lời câu hỏi trên nhé!
Bài 18 :
Mặt sân cỏ trong sân vận động Quốc gia Mỹ Đình có dạng hình chữ nhật có chiều dài 105 m và chiều rộng 68 m. Nam vẽ mô phỏng mặt sân cỏ này bằng một hình chữ nhật có chiều dài 21 cm và chiều rộng 13,6 cm. Hỏi Nam đã vẽ mô phỏng mặt sân đúng tỉ lệ hay chưa?
Bài 19 :
Thay tỉ số sau đây bằng tỉ số giữa các số nguyên:
\(a)\dfrac{{10}}{{16}}:\dfrac{4}{{21}};b)1,3:2,75;c)\dfrac{{ - 2}}{5}:0,25\)
Bài 20 :
Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức:
\(12:30;\dfrac{3}{7}:\dfrac{{18}}{{24}};2,5:6,25\)\(12:30;\dfrac{3}{7}:\dfrac{{18}}{{24}};2,5:6,25\)
Bài 21 :
Lập tất cả các tỉ lệ thức có thể được từ đẳng thức 14.(-15)= (-10).21
Bài 22 :
Để pha nước muối sinh lí, người ta cần pha theo đúng tỉ lệ. Biết rằng cứ 3 l nước tinh khiết thì pha với 27 g muối. Hỏi nếu có 45 g muối thì cần pha với bao nhiêu lít nước tinh khiết để được nước muối sinh lí?
Bài 23 :
Lập các tỉ lệ thức có thể được từ đẳng thức 3x = 4y (x,y \( \ne \)0)
Bài 24 :
Hãy lập tất cả các tỉ lệ thức có thể được từ 4 số: 5; 10; 25; 50
Bài 25 :
Lập tất cả các tỉ lệ thức có thể được từ bốn số sau: 0,2; 0,3; 0,8; 1,2.
Bài 26 :
Từ tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) ( với a,b,c,d khác 0) có thể suy ra những tỉ lệ thức nào?
Bài 27 :
Cho hai máy tính xách tay (laptop) có kích thước màn hình (tính theo đơn vị mm) lần lượt là 227,6 × 324 và 170,7 × 243. Tính tỉ số giữa chiều rộng và chiều dài của mỗi màn hình.
Bài 28 :
a) Từ các tỉ số \(\dfrac{6}{5}:2\) và \(\dfrac{{12}}{5}:4\) có lập được một tỉ lệ thức hay không?
b) Hãy lập hai tỉ lệ thức từ bốn số 9;2;3;6.
Bài 29 :
Chứng minh các tỉ số giữa chiều rộng và chiều dài của màn hình hai loại máy tính đã nêu trong HĐ 1 sẽ tạo thành 1 tỉ lệ thức.
Bài 30 :
Tìm các tỉ số bằng nhau trong các tỉ số sau đây rồi lập tỉ lệ thức:
\(7 : 21\); \(\dfrac{1}{5}:\dfrac{1}{2}\); \(\dfrac{1}{4}: \dfrac{3}{4}\); \(1,1 : 3,2; 1 : 2,5\)


















Danh sách bình luận