Đề bài

Cho tam giác ABC cân tại đỉnh A với $\widehat A = {80^0}$. Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?

• A. DE // BC        
• B. $\widehat B = {50^0}$
• C. $\widehat {ADE} = {50^0}$
• D. Cả ba phát biểu trên đều sai

Phương pháp giải

Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song

Lời giải của GV Loigiaihay.com

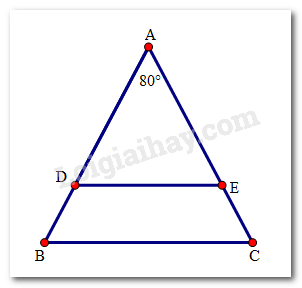
Do tam giác ABC cân tại A nên $\widehat B = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{80}^0}}}{2} = {50^0}$

Ta thấy tam giác ADE cân do AD = AE

$\Rightarrow \widehat {ADE} = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{80}^0}}}{2} = {50^0}$

Do đó $\widehat B = \widehat {ADE}$ .

Mà hai góc này ở vị trí đồng vị nên ED // BC ( Dấu hiệu nhận biết 2 đường thẳng song song)

Vậy D là đáp án sai.

Đáp án : D