Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Áp dụng tính chất tổng ba góc của một tam giác
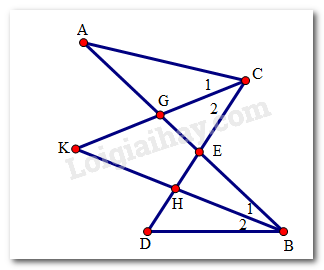
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE.
Xét tam giác KGB và tam giác AGC và theo tính chất góc ngoài của tam giác ta có:
\(\widehat K + \widehat {{B_1}} = \widehat {AGK}\)
\(\widehat A + \widehat {{C_1}} = \widehat {AGK}\)
Do đó \(\widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1)
Xét tam giác KHC và tam giác DHB và theo tính chất góc ngoài của tam giác ta có:
\(\widehat K + \widehat {{C_2}} = \widehat {EHB}\)
\(\widehat D + \widehat {{B_2}} = \widehat {EHB}\)
Do đó \(\widehat K + \widehat {{C_2}} = \widehat D + \widehat {{B_2}}\) (2)
Do \(\widehat {{B_1}} = \widehat {{B_2}}\) (BK là tia phân giác của góc DBA);
\(\widehat {{C_1}} = \widehat {{C_2}}\) (CK là tia phân giác của góc ACD).
Nên cộng (1) với (2) ta được \(2\widehat K = \widehat A + \widehat D\), do đó \(\widehat K = \frac{{\widehat A + \widehat D}}{2}\) hay \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Bài 2 :
Cho hình vẽ sau. Tính số đo góc x:
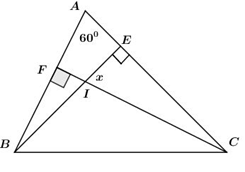
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Bài 3 :
Khẳng định nào sau đây là sai?
-
A.
Tam giác tù là tam giác có 1 góc tù
-
B.
Tam giác nhọn là tam giác có 3 góc đều là góc nhọn
-
C.
Góc lớn nhất trong 1 tam giác là góc tù
-
D.
2 góc nhọn trong tam giác vuông phụ nhau.
Bài 4 :
Cho tam giác nhọn ABC có 3 góc bằng nhau. Tính số đo góc C
-
A.
\({60^0}\)
-
B.
\({50^0}\)
-
C.
\({45^0}\)
-
D.
\({90^0}\)
Bài 5 :
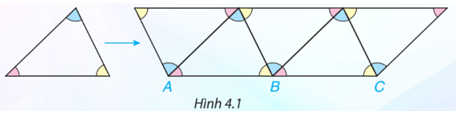
Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1. Em có nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác? Từ đó em rút ra kết luận gì về vị trí của ba điểm A, B, C?
Bài 6 :
Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.
- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
Bài 7 :
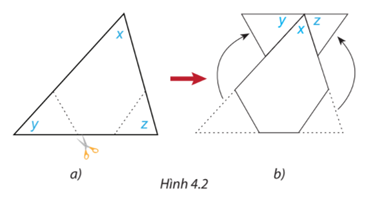
Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc \(x\) như Hình \(4.2\;{\rm{b}}\). Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.
Bài 8 :
Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?
Bài 9 :
Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Bài 10 :
Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5)
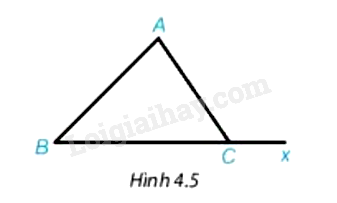
Chứng minh rằng \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)
Bài 11 :
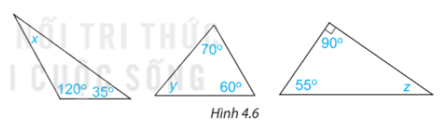
Tính các số đo x, ,y ,z trong Hình 4.6
Bài 12 :
Trong các tam giác (H.4.7), tam giác nào là tam giác nhọn, tam giác tù?
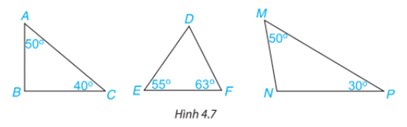
Bài 13 :
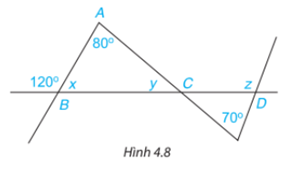
Tính các số đo x, y, z trong Hình 4.8
Bài 14 :
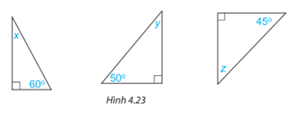
Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?
Bài 15 :
Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.
Bài 16 :
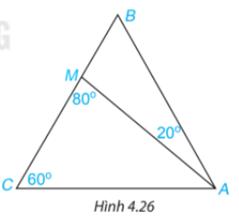
Cho tam giác ABC có \(\widehat {BCA} = {60^o}\) và điểm M nằm trên cạnh BC sao cho \(\widehat {BAM} = {20^\circ },\widehat {AMC} = {80^\circ }({\rm{H}}.4.26).\) Tính số đo các góc AMB, ABC, BAC.
Bài 17 :
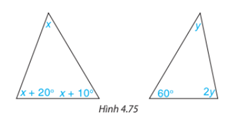
Tính các số đo x, y trong tam giác dưới đây (H.4.75)
Bài 18 :
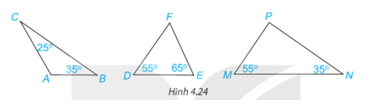
Hãy tính các số đo các góc A, D, N trong các tam giác dưới đây (H.4.3). Trong các tam giác đó, hãy chỉ ra tam giác nào là nhọn, tù, vuông.
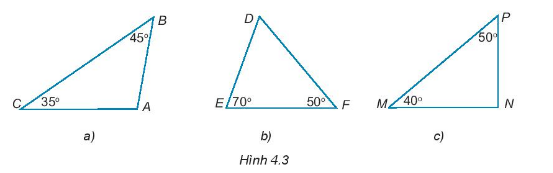
Bài 19 :
Trong các tam giác dưới đây (H.4.4), tam giác nào là nhọn, vuông, tù?
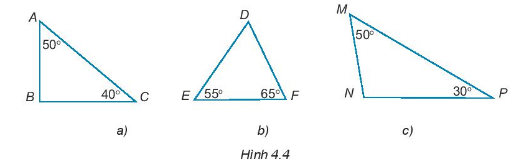
Bài 20 :
Hãy viết các góc A, B, C của tam giác ABC theo thứ tự tăng dần trong các trường hợp sau:
a) \(\widehat A = {60^0};\widehat B > \widehat A\)
b) \(\widehat A = {55^0};\widehat B < \widehat A\)
Bài 21 :
Hãy viết các góc A, B, C của tam giác ABC theo thứ tự giảm dần trong các trường hợp sau:
a) \(\widehat A = {60^0};\widehat B < \widehat A\)
b) \(\widehat A > {90^0};\widehat B > {45^0}\)
Bài 22 :
Tính tổng số đo \(\widehat A + \widehat C\) trong hình 4.8.
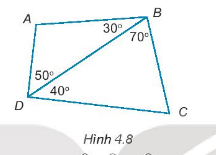
Bài 23 :
Cho tam giác ABC thoả mãn \(\widehat A = \widehat B = 2\widehat C\)
a) Tính số đo các góc của tam giác ABC.
b) Tam giác ABC là tam giác nhọn, tù hay vuông?
Bài 24 :
Trong các câu sau đây, câu nào đúng?
A. Mọi tam giác có ít nhất một góc tù.
B. Mọi tam giác có ít nhất hai góc nhọn.
C. Mọi tam giác cân có một góc bằng 60 độ.
D. Tam giác vuông cân có hai góc vuông.
Bài 25 :
Trong các câu sau đây, câu nào sai?
A. Tổng số đo ba góc trong một tam giác bằng 180 độ.
B. Tổng số đo hai góc nhọn trong một tam giác vuông bằng 90 độ.
C. Tổng số đo hai góc nhọn trong một tam giác tù lớn hơn 90 độ.
D. Góc lớn nhất trong tam giác nhọn có số đo nhỏ hơn 90 độ.
Bài 26 :
Tính số đo các góc x, y, z, t, v trong hình 4.55
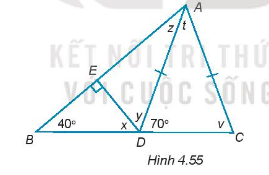
Bài 27 :
Trong các câu sau đây, câu nào đúng, câu nào sai?
a) Tam giác nhọn có ba góc đều nhọn.
b) Tam giác vuông có đúng hai góc nhọn.
c) Tam giác tù có đúng một góc nhọn.
d) Trong ba góc của một tam giác tù, góc tù có số đo lớn nhất.
Bài 28 :
Trong các câu sau đây, câu nào đúng, câu nào sai?
a) Tam giác cân có một góc bằng 60 độ là tam giác đều.
b) Tam giác cân là tam giác nhọn.
c) Tổng hai góc nhọn của một tam giác vuông bằng 90 độ.
d) Tam giác vuông cân thì luôn cân tại đỉnh góc vuông và có hai góc nhọn bằng 45 độ.
Bài 29 :
Tính số đo các góc chưa biết của các tam giác dưới đây (h.4.56)
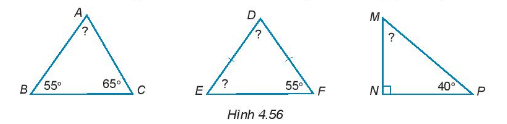
Bài 30 :
Trong một tam giác tù có tất cả bao nhiêu góc nhọn?
A. 0
B. 1
C. 2
D. 3


















Danh sách bình luận