Trên mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C(-1;0). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC.
-
A.
(0;0)
-
B.
(1;0)
-
C.
(2;0)
-
D.
(3;0)
- Viết phương trình đường thẳng \(BC\), tham số hóa tọa độ điểm \(M \in BC\) theo tham số \(m\).
- Viết phương trình đường thẳng \(AM\) theo \(m\).
- Tính \(d\left( {B;AM} \right)\) và \(d\left( {C;AM} \right)\). Sử dụng công thức khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(ax + by + c = 0\) là \(d\left( {M;AB} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
- Để \({S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\), giải phương trình tìm \(m\).
Phương trình đường thẳng \(BC\) là \(y = 0\), vì \(M \in BC\) nên gọi \(M\left( {m;0} \right)\).
Ta có: \(\overrightarrow {AM} = \left( {m - 2; - 3} \right)\) nên \(\overrightarrow n = \left( {3;m - 2} \right)\) là 1 VTPT của đường thẳng \(AM\).
Phương trình đường thẳng \(AM\) là:
\(\begin{array}{l}3\left( {x - 2} \right) + \left( {m - 2} \right)\left( {y - 3} \right) = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 6 - 3m + 6 = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 3m = 0\end{array}\)
\(\begin{array}{l} \Rightarrow d\left( {B;AM} \right) = \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\\,\,\,\,\,\,d\left( {C;AM} \right) = \dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\end{array}\)
Ta có: \(\left\{ \begin{array}{l}{S_{\Delta MAB}} = \dfrac{1}{2}d\left( {B;AM} \right).AM\\{S_{\Delta MAC}} = \dfrac{1}{2}d\left( {C;AM} \right).AM\end{array} \right. \Rightarrow {S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\).
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }} = 2\dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\ \Leftrightarrow \left| {15 - 3m} \right| = 2\left| { - 3 - 3m} \right|\\ \Leftrightarrow \left[ \begin{array}{l}15 - 3m = - 6 - 6m\\15 - 3m = 6 + 6m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 7\\m = 1\end{array} \right.\end{array}\)
Vậy \(M\left( {1;0} \right)\) hoặc \(M\left( { - 7;0} \right)\).
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Khoảng cách từ giao điểm của hai đường thẳng \(x - 3y + 4 = 0\) và \(2x + 3y - 1 = 0\) đến đường thẳng $\Delta :3x + y + 4 = 0$ bằng:
-
A.
$2\sqrt {10} $.
-
B.
$\dfrac{{3\sqrt {10} }}{5}$.
-
C.
$\dfrac{{\sqrt {10} }}{5}$.
-
D.
\(2\).
Bài 2 :
Lập phương trình đường thẳng \(\Delta\) đi qua M(2;7) và cách N(1;2) một khoảng bằng 1.
-
A.
$12x - 5y + 11= 0$
-
B.
$x - 5y + 11 = 0$
-
C.
$12x - 5y + 11 = 0$ và \(x-2=0\)
-
D.
$19x - 5y + 11 = 0$
Bài 3 :
Cho đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 3}}{{ - 1}}\) và điểm \(N\left( {1;\, - 4} \right)\). Khoảng cách từ điểm \(N\) đến đường thẳng \(\Delta \) bằng
-
A.
\(\dfrac{2}{5}\).
-
B.
\(\dfrac{{2\sqrt 5 }}{5}\).
-
C.
\(2\).
-
D.
\(\dfrac{2}{{\sqrt {17} }}\).
Bài 4 :
Cho hai đường thẳng song ${d_1}:5x - 7y + 4 = 0\,\,$và ${d_2}:5x - 7y + 6 = 0.\,\,$Khoảng cách giữa \({d_1}\) và \({d_2}\) là
-
A.
\(\dfrac{4}{{\sqrt {74} }}\).
-
B.
\(\dfrac{6}{{\sqrt {74} }}\).
-
C.
\(\dfrac{2}{{\sqrt {74} }}\).
-
D.
\(\dfrac{{10}}{{\sqrt {74} }}\).
Bài 5 :
Khoảng cách từ điểm M(–2;2) đến đường thẳng Δ: \(5x - 12y + 8 = 0\) bằng
-
A.
\(\dfrac{2}{{13}}\)
-
B.
\(2\)
-
C.
\(13\)
-
D.
\(14\)
Bài 6 :
Tính khoảng cách từ điểm \(M\left( {1;2} \right)\) đến đường thẳng\(\Delta :\left\{ \begin{array}{l}x = 5 + 3t\\y = - 5 - 4t\end{array} \right.\).
Bài 7 :
Đo trực tiếp khoảng cách từ điểm M đến đường thẳng A(H7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4.
Bài 8 :
Cho điểm \(M\left( {{x_o};{y_0}} \right)\) và đường thẳng \(\Delta :{\rm{a}}x + by + c = 0\) có vecto pháp tuyến \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right)\)
Gọi H là hình chiếu vuông góc của M trên \(\Delta \).
a) Chưng minh rằng \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\)
b) Giả sử H có tọa độ \(\left( {{x_1};{y_1}} \right)\). Chứng minh rằng \(\overrightarrow n .\overrightarrow {HM} = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\)
c) Chứng minh rằng \(HM = \frac{{\left| {{\rm{a}}{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Bài 9 :
Tính khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\).
Bài 10 :
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là \(A(1;1),B(5;2),C(4;4)\). Tính độ dài các đường cao của tam giác ABC.
Bài 11 :
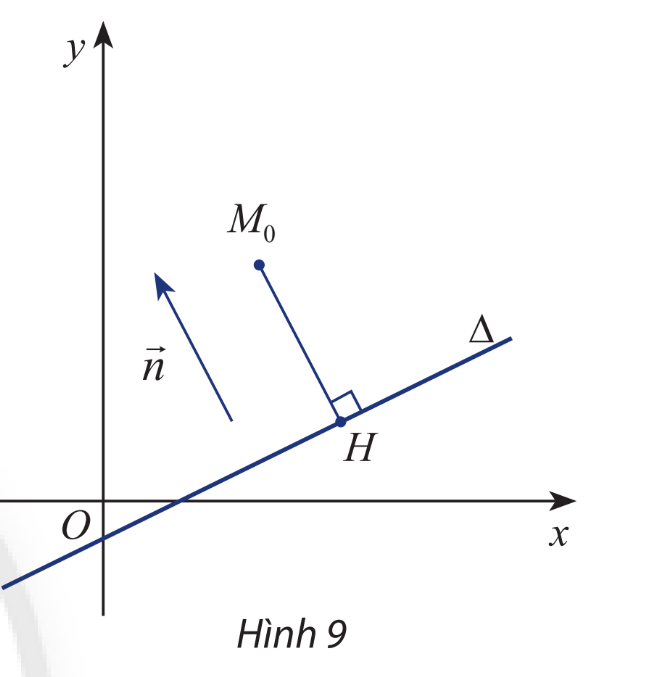
Trong mặt phẳng Oxy. Cho đường thẳng \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) có vectơ pháp tuyến \(\overrightarrow n \) và cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) có hình chiếu vuông góc \(H\left( {{x_H};{y_H}} \right)\)trên \(\Delta \)(hình 9).
a) Chứng minh rằng hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \) cùng phương và tìm tọa độ của chúng.
b) Gọi p là tích vô hướng của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \).
Chứng minh rằng \(p = a{x_0} + b{y_0} + c\).
c) Giải thích công thức \(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\).
Bài 12 :
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M(1;2)\) và \(\Delta :3x - 4y + 12 = 0\)
b) \(M(4;4)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = - t\end{array} \right.\)
c) \(M(0;5)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = \frac{{ - 19}}{4}\end{array} \right.\)
d) \(M(0;0)\) và \(\Delta :3x + 4y - 25 = 0\)
Bài 13 :
Tính khoảng cách giữa hai đường thẳng \(\Delta :3x + 4y - 10 = 0\) và \(\Delta ':6x + 8y - 1 = 0\).
Bài 14 :
Trong mặt phẳng Oxy cho điểm \(S(x;y)\) di động trên đường thẳng \(d:12x - 5y + 16 = 0\). Tính khoảng cách ngắn nhất từ điểm \(M(5;10)\) đến điểm S.
Bài 15 :
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y - 13 = 0\) và \(\Delta ':3x + 4y - 27 = 0\).
Bài 16 :
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\) và \({\Delta _2}:x - y - 1 = 0\)
Bài 17 :
Tính khoảng cách từ một điểm đến một đường thẳng trong mỗi trường hợp sau:
a) \(A\left( {1; - 2} \right){\rm{ }}v\`a {\rm{ }}{\Delta _1}:{\rm{ }}3x - y + {\rm{ }}4{\rm{ }} = {\rm{ }}0\);
b) B(-3; 2) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 2 + t\\y = 1 - 2t\end{array} \right.\)
Bài 18 :
Khoảng cách từ điểm \(A\left( {1;1} \right)\) đến đường thẳng \(\Delta :3x + 4y + 13 = 0\) bằng:
A. 1
B. 2
C. 3
D. 4
Bài 19 :
Trong mặt phẳng \(Oxy\), tìm điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng \(\Delta :3x + y - 3 = 0\) bằng \(\sqrt {10} \).
Bài 20 :
Cho điểm \(A\left( {2;3} \right)\) và đường thẳng \(d:x + y + 3 = 0\). Khoảng cách từ điểm A đến đường thẳng d là:
A. \(\frac{8}{{\sqrt {13} }}\)
B. \(4\sqrt 2 \)
C. 8
D. \(2\sqrt 2 \)
Bài 21 :
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M\left( {2;3} \right)\) và \(\Delta :8x - 6y + 7 = 0\).
b) \(M\left( {0;1} \right)\) và \(\Delta :4x + 9y - 20 = 0\).
c) \(M\left( {1;1} \right)\) và \(\Delta :3y - 5 = 0\).
d) \(M\left( {4;9} \right)\) và \(\Delta :x - 25 = 0\).
Bài 22 :
Tìm c để đường thẳng \(\Delta :4x - 3y + c = 0\) tiếp xúc với đường tròn \(\left( C \right)\) có \(J\left( {1;2} \right)\) và bán kính \(R = 3\).
Bài 23 :
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y - 11 = 0\) và \(\Delta ':6x + 8y - 1 = 0\).
Bài 24 :
Một trạm viễn thông \(S\) có tọa độ \(\left( {5;1} \right)\). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng \(\Delta \) có phương trình \(12x + 5y - 20 = 0\). Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông \(S\). Biết rằng mỗi đơn vị độ dài tương ứng với 1 km.
Bài 25 :
Bán kính của đường tròn tâm \(I\left( {0; - 2} \right)\) và tiếp xúc với đường thẳng \(\Delta :3x - 4y - 23 = 0\) là:
A. 15
B. 5
C. \(\frac{3}{5}\)
D. 3
Bài 26 :
Tính khoảng cách giữa hai đường thẳng \(\Delta :ax + by + c = 0\) và \(\Delta ':ax + by + d = 0\) (biết \(\Delta //\Delta '\)).
Bài 27 :
Khoảng cách từ điểm M(5;–2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:
A. 13
B. \(\sqrt {13} \)
C. \(\frac{{\sqrt {13} }}{{13}}\)
D. \(2\sqrt {13} \)
Bài 28 :
Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:
a) A(−3 ; 1) và ∆1: 2x + y - 4 = 0.
b) B(1; -3) và ∆2: \(\left\{ \begin{array}{l}x = - 3 + 3t\\y = 1 - t\end{array} \right.\).
Bài 29 :
Cho hai đường thẳng song song ∆1: ax + by + c = 0 và ∆2: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆1 và ∆2 bằng \(\frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Bài 30 :
Khoảng cách từ điểm M(4 ; –2) đến đường thẳng ∆: x − 2y + 2 = 0 bằng:
A. \(\frac{{2\sqrt 5 }}{5}\)
B. \(2\sqrt 5 \)
C. 2
D. \(\sqrt 5 \)


















Danh sách bình luận