Đề bài

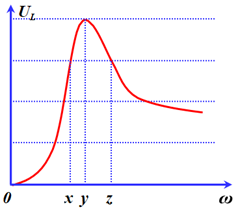
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P₁, P₂ và P₃. Biểu thức nào sau đây đúng?

• A. \(\dfrac{{{P_1} + {P_3}}}{8} = \dfrac{{{P_2}}}{9}\).
• B. \(\dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}\).
• C. \(\dfrac{{{P_1} + {P_2}}}{{16}} = \dfrac{{{P_3}}}{9}\).
• D. \(\dfrac{{{P_1} + {P_2}}}{9} = \dfrac{{{P_3}}}{{16}}\).

Phương pháp giải

Sử dụng kĩ năng đọc đồ thị

Điện áp U_Lmax khi tần số có giá trị ω₂

Hai tần số ω₁, ω₃ cho cùng giá trị điện áp \({U_L}:\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}\)

Độ lệch pha giữa điện áp và cường độ dòng điện: \(\cos \varphi  = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)

Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)

Công suất tiêu thụ: \(P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R}\)

Lời giải của GV Loigiaihay.com

Điện áp hiệu dụng giữa hai đầu cuộn dây là:

\({U_L} = \dfrac{{U.{Z_L}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}}}{R}.\dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{U.{Z_L}.cos\varphi }}{R}\)

Với tần số ω₁ = x; ω₂ = y và ω₃ = z, ta có:

\(\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}} = \dfrac{2}{{{\omega _2}^2}}\)

Từ đồ thị ta thấy:

\(\begin{array}{l}{U_{L1}} = {U_{L3}} = \dfrac{3}{4}{U_{L2}} = \dfrac{3}{4}{U_{L\max }}\\ \Rightarrow \dfrac{{U.{Z_{L1}}\cos {\varphi _1}}}{R} = \dfrac{{U.{Z_{L3}}\cos {\varphi _3}}}{R} = \dfrac{3}{4}\dfrac{{U.{Z_{L2}}\cos {\varphi _2}}}{R}\\ \Rightarrow {\omega _1}^2{\cos ^2}{\varphi _1} = {\omega _3}^2{\cos ^2}{\varphi _3} = \dfrac{9}{{16}}{\omega _2}^2{\cos ^2}{\varphi _2}\\ \Rightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _1}^2}}\\\dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}\varphi }} = \dfrac{9}{{16}}\dfrac{{{\omega ^2}}}{{{\omega _2}^2}}\end{array} \right. \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _3}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega ^2}.\left( {\dfrac{1}{{{\omega _1}^2}} + \dfrac{1}{{{\omega _3}^2}}} \right)\\ \Rightarrow \dfrac{{{{\cos }^2}{\varphi _1}}}{{{{\cos }^2}{\varphi _2}}} + \dfrac{{{{\cos }^2}{\varphi _2}}}{{{{\cos }^2}{\varphi _2}}} = \dfrac{9}{{16}}{\omega _2}^2.\dfrac{2}{{{\omega _2}^2}} = \dfrac{9}{8}\,\,\left( 1 \right)\end{array}\)

Công suất tiêu thụ của mạch điện là:

\(P = \dfrac{{{U^2}{{\cos }^2}\varphi }}{R} \Rightarrow P \sim {\cos ^2}\varphi \)

Từ (1) ta có: \(\dfrac{{{P_1}}}{{{P_2}}} + \dfrac{{{P_3}}}{{{P_2}}} = \dfrac{9}{8} \Rightarrow \dfrac{{{P_1} + {P_3}}}{9} = \dfrac{{{P_2}}}{8}\)

Đáp án : B