Cho các điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?
-
A.
\(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {CA} \).
-
B.
\(\overrightarrow {AB} = \overrightarrow {CB} + \overrightarrow {AC} \).
-
C.
\(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {AC} \).
-
D.
\(\overrightarrow {AB} = \overrightarrow {CA} + \overrightarrow {BA} \).
Sử dụng quy tắc ba điểm $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $.
\(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {AC} \).
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
-
A.
\(\overrightarrow {AB} + \overrightarrow {IA} = \overrightarrow {BI} \).
-
B.
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \).
-
C.
\(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\).
-
D.
\(\overrightarrow {AB} + \overrightarrow {BD} = \vec 0\).
Bài 2 :
Cho các điểm \(A,B,C,M,N,P\) phân biệt. Khẳng định nào sau đây đúng?
-
A.
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} .\)
-
B.
\(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NP} .\)
-
C.
\(\overrightarrow {CA} + \overrightarrow {BA} = \overrightarrow {CB} .\)
-
D.
\(\overrightarrow {AA} + \overrightarrow {BB} = \overrightarrow {AB} .\)
Bài 3 :
Mệnh đề nào sau đây sai?
-
A.
Nếu \(M\) là trung điểm đoạn thẳng \(AB\) thì \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
-
B.
Nếu \(G\) là trọng tâm tam giác \(ABC\) thì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 .\)
-
C.
Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CA} .\)
-
D.
Nếu ba điểm phân biệt \(A,\;B,\;C\) nằm tùy ý trên một đường thẳng thì \(\left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right|.\)
Bài 4 :
Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.
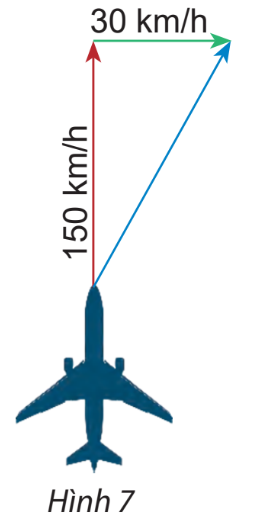
Bài 5 :
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Bài 6 :
Cho các điểm A, B, O. Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} = \overrightarrow {OA} - \overrightarrow {OB} \)
B. \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \)
C. \(\overrightarrow {AB} = \overrightarrow {OA} + \overrightarrow {OB} \)
D. \(\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \)
Bài 7 :
Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh \(\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} + \overrightarrow {BD} \) (*)


















Danh sách bình luận