Đề bài

Cho biểu thức \(P =  - a + \sqrt a \) với \(a \ge 0\). Mệnh đề nào sau đây là mệnh đề đúng?

• A. Giá trị nhỏ nhất của $P$ là \(\dfrac{1}{4}\).
• B. Giá trị lớn nhất của $P$  là \(\dfrac{1}{4}\).
• C. Giá trị lớn nhất của $P$ là \(\dfrac{1}{2}\).
• D. $P$ đạt giá trị nhỏ nhất tại \(a = \dfrac{1}{2}\)

Phương pháp giải

- Biến đổi biểu thức \(P\) về dạng hằng đẳng thức ẩn với \(\sqrt a \).

- Đánh giá GTLN hoặc GTNN của \(P\) dựa vào chú ý bình phương của một biểu thức luôn lớn hơn hoặc bằng \(0\).

Lời giải của GV Loigiaihay.com

Ta có: \(P =  - a + \sqrt a  =  - {\left( {\sqrt a } \right)^2} + \sqrt a  = \dfrac{1}{4} - {\left( {\sqrt a  - \dfrac{1}{2}} \right)^2} \le \dfrac{1}{4}\)

Vậy GTLN của $P$ là \(\dfrac{1}{4}\) đạt được tại $a=\dfrac{1}{4}$.

Ta sẽ chứng minh \(P\) không có GTNN.

Đặt \(\sqrt a  = t \ge 0\) thì \(P =  - {t^2} + t\)

Xét hàm số bậc hai \(y = f\left( t \right) =  - {t^2} + t\) trên \(\left[ {0; + \infty } \right)\) ta có \(t =  - \dfrac{b}{{2a}} = \dfrac{1}{2}\)

Bảng biến thiên:

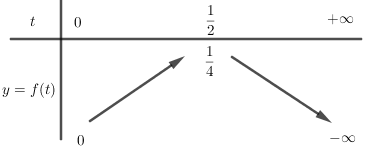
Từ bảng biến thiên ta thấy hàm số không đạt GTNN hay không tồn tại GTNN của \(P\).

Kết luận: \(P\) đạt GTLN bằng \(\dfrac{1}{4}\) tại \(a = \dfrac{1}{4}\) và không có GTNN.

Đáp án : B