Tập nghiệm của bất phương trình \(2x\left( {2 - x} \right) \ge 2 - x\) là
-
A.
\(\left[ {\dfrac{1}{2};2} \right]\)
-
B.
\(\left[ {\dfrac{1}{2}; + \infty } \right)\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( { - \infty ;\dfrac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\)
Giải bất phương trình bằng phương pháp đưa về phương trình tích và dùng quy tắc xét dấu của tam thức bậc hai để tìm nghiệm của bất phương trình.
\(\begin{array}{l}2x\left( {2 - x} \right) \ge 2 - x \Leftrightarrow 2x\left( {x - 2} \right) \le x - 2\\ \Leftrightarrow \left( {x - 2} \right)\left( {2x - 1} \right) \le 0 \Leftrightarrow \dfrac{1}{2} \le x \le 2.\end{array}\)
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)
-
A.
\(S = 0.\)
-
B.
\(S = \left\{ 0 \right\}.\)
-
C.
\(S = \emptyset .\)
-
D.
\(S = \mathbb{R}.\)
Bài 2 :
Cho bất phương trình \({x^2} - 8x + 7 \ge 0\). Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình?
-
A.
\(\left( { - \infty ;0} \right].\)
-
B.
\(\left[ {8; + \infty } \right).\)
-
C.
\(\left( { - \infty ;1} \right].\)
-
D.
\(\left[ {6; + \infty } \right).\)
Bài 3 :
Bất phương trình nào sau đây có tập nghiệm là \(\mathbb{R}\)?
-
A.
\( - 3{x^2} + x - 1 \ge 0.\)
-
B.
\( - 3{x^2} + x - 1 > 0.\)
-
C.
\( - 3{x^2} + x - 1 < 0.\)
-
D.
\(3{x^2} + x - 1 \le 0.\)
Bài 4 :
Tập hợp nào dưới đây chứa phần tử không là nghiệm của bất phương trình $\sqrt 2 {x^2} - \left( {\sqrt 2 + 1} \right)x + 1 < 0$?
-
A.
$\left( {\dfrac{{\sqrt 2 }}{2};1} \right)$
-
B.
$\left( {\dfrac{{\sqrt 2 }}{2};\dfrac{1}{2}} \right)$
-
C.
$\left[ {\dfrac{{\sqrt 2 }}{2};1} \right]$
-
D.
$\left( {\dfrac{{\sqrt 3 }}{2};1} \right)$
Bài 5 :
Bất phương trình \({x^2} - 6\sqrt 2 x + 18 \ge 0\) có tập nghiệm là:
-
A.
\(S = \mathbb{R}\)
-
B.
\(S = \emptyset \)
-
C.
\(S = \left( {3\sqrt 2 ;\,\, + \infty } \right)\)
-
D.
\(S = \mathbb{R}\backslash \left\{ {3\sqrt 2 } \right\}\)
Bài 6 :
Tập nghiệm của bất phương trình \({x^2} + 5x - 6 \le 0\) là:
-
A.
\(\left[ { - {\rm{ 6}};{\rm{1}}} \right]\).
-
B.
\(\left[ {{\rm{2}};{\rm{3}}} \right]\).
-
C.
\(\left( { - \infty ;{\rm{6}}} \right] \cup \left[ {{\rm{1}}; + \infty } \right)\).
-
D.
\(\left( { - \infty ;{\rm{2}}} \right] \cup \left[ {{\rm{3}}; + \infty } \right)\).
Bài 7 :
Tập nghiệm của bất phương trình \( - {x^2} + 5x + 6 > 0\) là:-
A.
\(\left( { - 1;6} \right)\)
-
B.
\(\left\{ { - 1;6} \right\}\)
-
C.
\(\left[ { - 1;6} \right]\)
-
D.
\(\left( { - \infty ; - 1} \right) \cup \left( {6; + \infty } \right)\)
Bài 8 :
Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
Bài 9 :
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).
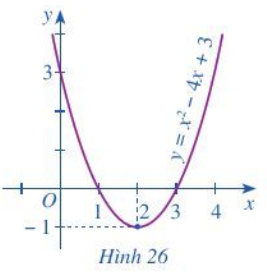
Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Bài 10 :
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
Bài 11 :
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Bài 12 :
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 5x + 3 > 0\)
b) \( - {x^2} - 2x + 8 \le 0\)
c) \(4{x^2} - 12x + 9 < 0\)
d) \( - 3{x^2} + 7x - 4 \ge 0\)
Bài 13 :
Tìm m để phương trình \(2{x^2} + \left( {m + 1} \right)x + m - 8 = 0\) có nghiệm.
Bài 14 :
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
Bài 15 :
Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là:
-
A.
(1; 2)
-
B.
\(\left( {-\infty ;{\rm{ }}1} \right){\rm{ }} \cup {\rm{ }}\left( {2;{\rm{ }} + \infty } \right)\)
-
C.
\(\left( {-\infty ;{\rm{ }}1} \right)\)
-
D.
\(\left( {2;{\rm{ }} + \infty } \right)\)
Bài 16 :
Tập nghiệm của bất phương trình \({x^2}-{\rm{ }}1{\rm{ }} > {\rm{ }}0\) là:
-
A.
\(\left( {1; + \infty } \right)\)
-
B.
\(\left( { - 1; + \infty } \right)\)
-
C.
(– 1; 1);
-
D.
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
Bài 17 :
Tập nghiệm của bất phương trình \( - {x^2} + 3x + 18 \ge 0\) là:
A. \(\left[ { - 3;6} \right]\)
B. \(\left( { - 3;6} \right)\)
C. \(x \in \left( { - \infty ; - 3} \right) \cup \left( {6; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 3} \right] \cup \left[ {6; + \infty } \right)\)
Bài 18 :
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 8x + 5 > 0\)
b) \( - 2{x^2} - x + 3 \le 0\)
c) \(25{x^2} - 10x + 1 < 0\)
d) \( - 4{x^2} + 5x + 9 \ge 0\)
Bài 19 :
Tìm giao các tập nghiệm của hai bất phương trình \( - 3{x^2} + 7x + 10 \ge 0\) và \( - 2{x^2} - 9x + 11 > 0\).
Bài 20 :
Tìm \(m\) để phương trình \( - {x^2} + \left( {m + 2} \right)x + 2m - 10 = 0\) có nghiệm.
Bài 21 :
Tập nghiệm của bất phương trình \( - 5{x^2} + 6x + 11 \le 0\) là:
A. \(\left[ { - 1;\frac{{11}}{5}} \right]\)
B. \(\left( { - 1;\frac{{11}}{5}} \right)\)
C. \(x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\)
Bài 22 :
Giải các bất phương trình bậc hai sau:
a) \(4{x^2} - 9x + 5 \le 0\)
b) \( - 3{x^2} - x + 4 > 0\)
c) \(36{x^2} - 12x + 1 > 0\)
d) \( - 7{x^2} + 5x + 2 < 0\)
Bài 23 :
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Bài 24 :
Giải các bất phương trình bậc hai:
a) \({x^2} - 1 \ge 0\)
b) \({x^2} - 2x - 1 < 0\)
c) \( - 3{x^2} + 12x + 1 \le 0\)
d) \(5{x^2} + x + 1 \ge 0\)
Bài 25 :
Bất phương trình \({x^2} - 2mx + 4 > 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\) khi
A. \(m = - 1.\)
B. \(m = - 2.\)
C. \(m = 2.\)
D. \(m > 2.\)
Bài 26 :
Giải các bất phương trình sau:
a) \(2{x^2} - 3x + 1 > 0\)
b) \({x^2} + 5x + 4 < 0\)
c) \( - 3{x^2} + 12x - 12 \ge 0\)
d) \(2{x^2} + 2x + 1 < 0.\)
Bài 27 :
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Bài 28 :
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Bài 29 :
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
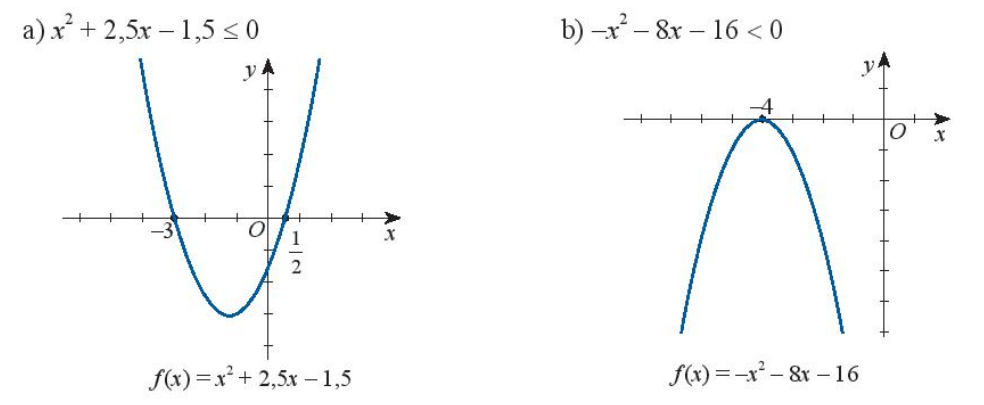
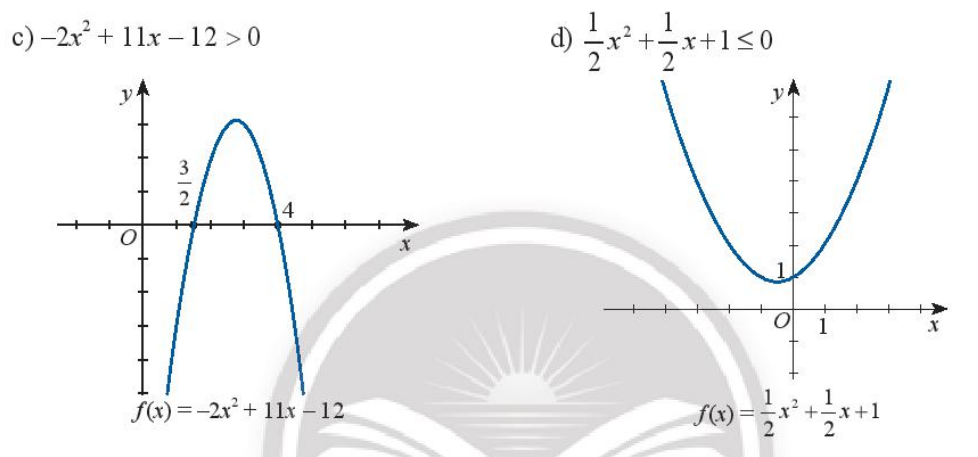
Bài 30 :
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 15x + 28 \ge 0\)
b) \( - 2{x^2} + 19x + 255 > 0\)
c) \(12{x^2} < 12x - 8\)
d) \({x^2} + x - 1 \ge 5{x^2} - 3x\)


















Danh sách bình luận