Khẳng định nào sau đây đúng?
-
A.
\(250 \vdots 25\)
-
B.
\(51 \vdots 7\)
-
C.
\(36 \vdots 16\)
-
D.
\(48 \vdots 18\)
Cho hai số tự nhiên \(a\) và \(b,\) trong đó \(b \ne 0,\) nếu có số tự nhiên \(x\) sao cho \(b.x = a\) thì ta nói \(a\) chia hết cho \(b\) và ta có phép chia hết \(a:b = x\), kí hiệu là \(a \vdots b\).
Ta có: 25.10=250 nên \(250 \vdots 25\)
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Khằng định nào sau đây sai?
-
A.
\(1698 \vdots 2\)
-
B.
\(1698 \vdots 3\)
-
C.
\(1698 \vdots 6\)
-
D.
\(1698 \vdots 5\)
Bài 2 :
Số nào trong các số sau chia hết cho 5
-
A.
120156
-
B.
555215
-
C.
5461
-
D.
1
Bài 3 :
Cô giáo muốn chia đều 40 học sinh thành các nhóm để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở (bỏ trống trong trường hợp không chia được).
Bài 4 :
Tìm kí hiệu thích hợp (\( \vdots ,\,\not{\vdots}\)) thay cho dấu “?”.
![]()
Bài 5 :
Lớp 6A có 6 tổ học sinh. Để tổ chức liên hoan cho lớp, cô Ngân đã mua 42 chiếc bánh ngọt và 45 quả quýt.
Cô Ngân có thể chia đều số bánh ngọt cho 6 tổ được không?
Cô Ngân có thể chia đều số quả quýt cho 6 tổ được không?
Bài 6 :
Tìm số tự nhiên x, biết x là bội của 9 và 20 < x < 40
Bài 7 :
Đội Sao đỏ của trường có 24 bạn. Cô phụ trách muốn chia đội thành các nhóm đều nhau để kiểm tra vệ sinh lớp học, mỗi nhóm có ít nhất 2 bạn. Em hãy chia giúp cô giáo bằng cách có thể.
Bài 8 :
Viết ngày và tháng sinh của em dưới dạng ngày a tháng b. Chỉ ra một ước của a và hai bội của b.
Bài 9 :
a) Thực hiện các phép tính: 9 . 0; 9 . 1; 9 . 2; 9 . 3; 9 . 4; 9 . 5; 9 . 6
b) Hảy chỉ ra bảy bội của 9.
Bài 10 :
a) Trong các số sau: 3,4,7,14,16,23,36,48,96, số nào là ước của 96?
b) Tìm các ước lớn hơn 10 của 115
c) Tìm các bội lớn hơn 100 và nhỏ hơn 200 của 15
d) Tìm các ước của 32
Bài 11 :
Cho các số 44, 7 345, 18 488, 66 713, 289 935, 1 987 650, 369 121 600.
a) Viết tập hợp A gồm các số chia hết cho 2 trong các số trên.
b) Viết tập hợp B gồm các số chia hết cho 5 trong các số trên
c) Viết tập hợp C gồm các số chia hết cho cả 2 và 5 trong các số trên
Bài 12 :
Chứng tỏ rằng:
a) (a+2 021).(a+2 020) là bội của 2 với mọi số tự nhiên a;
b) (2a+1).(2a+2).(2a+3) là bội của 3 với mọi số tự nhiên a
c) (7a)2020 là bội của 49 với mọi số tự nhiên a
Bài 13 :
Cho a, b là các số tự nhiên thỏa mãn điều kiện a chia 51 dư 2 và b chia 17 dư 3. Hỏi 2a+3b có là bội của 17 không?
Bài 14 :
Tìm kí hiệu thích hợp (\( \vdots \), \(\not{ \vdots }\)) thay vào các dấu “?”
56 7; 63
8; 1 975
25; 2 020
20; 2 021
3
Bài 15 :
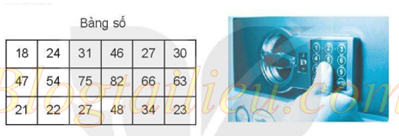
Để mở khóa két, Mai cần tìm được 8 chữ số ghép từ 4 số có hai chữ số, được cho trong bảng số dưới đây, các số đó được sắp xếp từ nhỏ đến lớn sao cho chúng chia hết cho 4 hoặc chia hết cho 5. Em hãy giúp Mai mở két nhé!
Bài 16 :
Khẳng định nào sau đây là đúng?
A. \(18 \vdots 3\) và \(20\not \vdots 4\)
B. \(18 \vdots 3\) và \(20 \vdots 4\)
C. \(18\not \vdots 3\) và \(20 \vdots 4\)
D. \(18\not \vdots 3\) và \(20\not \vdots 4\).
Bài 17 :
Cô giáo muốn chia lớp gồm 40 học sinh thành các nhóm để thực hiện các dự án học tập sao cho các nhóm có số người như nhau. Em hãy hoàn thành bảng sau (bỏ trống trong các trường hợp không chia được).
|
Số nhóm |
Số người ở một nhóm |
|
4 |
... |
|
... |
8 |
|
6 |
... |
|
8 |
... |
|
... |
4 |
Bài 18 :
Cô giáo có một số kẹo. Nếu cô chia số kẹo đó thành 12 phần như nhau thì dư 6 chiếc. Hỏi cô có thể chia số kẹo đó thành 4 phần mà không còn dư hay không?
Bài 19 :
Số tự nhiên A có hai chữ số thỏa mãn A chia cho 9 dư 1 và chia cho 10 dư 3. Khi đó, A chia cho 13 có số dư là bao nhiêu?


















Danh sách bình luận