Đề bài

Cho hình chóp tứ giác đều $S.ABCD$ có đường cao $SH = 6cm$, cạnh đáy bằng $4cm.$ Một mặt phẳng đi qua trung điểm $H’$ của $SH$ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ $S.A'B'C'D'$ và hình chóp cụt $ABCD.A'B'C'D'$

Câu 1

Tính thể tích của hình chóp $S.ABCD$.

A.

$32c{m^3}$

B.

$31\,c{m^3}$

C.

$16\,c{m^3}$

D.

$64\,c{m^3}$

Đáp án : A

Phương pháp giải

Sử dụng công thức thể tích hình chóp \(V = \dfrac{1}{3}S.h\) .

Lời giải của GV Loigiaihay.com

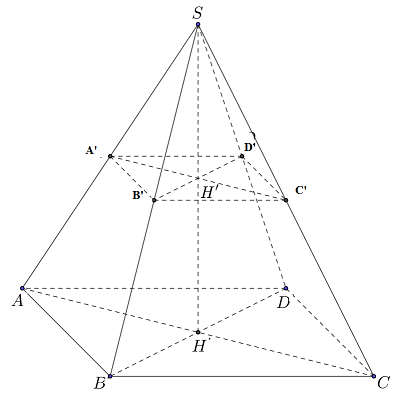
Thể tích hình chóp $S.ABCD$  bằng  \(\dfrac{1}{3}{.4^2}.6 = 32\,c{m^3}\) .

---

Xem thêm các câu hỏi cùng đoạn

Câu 2

Tính thể tích của hình chóp cụt \(ABCD.A'B'C'D'\) .

A.

$16\,c{m^3}$

B.

$28\,c{m^3}$

C.

$30\,c{m^3}$

D.

$4\,c{m^3}$

Đáp án : B

Phương pháp giải

Sử dụng cách tính thể tích hình chóp cụt:

Để tính thể tích của hình chóp cụt đều, ta lấy thể tích của hình chóp đều lớn trừ đi thể tích của hình chóp đều nhỏ.

Lời giải của GV Loigiaihay.com

Ta có \(SH' = \dfrac{1}{2}SH = \dfrac{1}{2}.6 = 3\,cm\)

Ta có \(SH' = HH'\)   nên  \(SA' = AA'\)  , tương tự \(SB' = BB'\)  Suy ra \(A'B' = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2\,cm\)

Thể tích hình chóp \(S.A'B'C'D'\)  bằng \(\dfrac{1}{3}{.2^2}.3 = 4\,c{m^3}\)  

Thể tích hình chóp cụt bằng \(32 - 4 = 28\,c{m^3}\) .

---