Đề bài

Viết phương trình tiếp tuyến của đồ thị hàm số $y =  - {x^4} + 6{x^2} - 5$ tại điểm cực tiểu của nó.

• A. $y = 5$
• B. $y =  - 5$
• C. $y = 0$            
• D. $y = x + 5$

Phương pháp giải

- Khảo sát hàm số $y =  - {x^4} + 6{x^2} - 5$ tìm điểm cực tiểu của đồ thị hàm số.

- Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu vừa tìm được.

Lời giải của GV Loigiaihay.com

Ta có: $y' =  - 4{{\text{x}}^3} + 12{\text{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 3 $ hoặc $x =  - \sqrt 3 $

Ta có bảng biến thiên

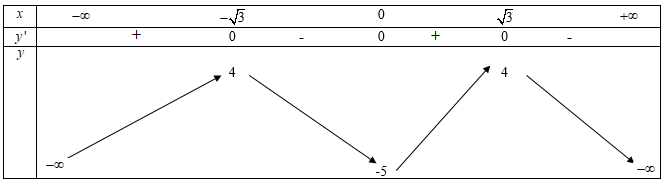
Quan sát bảng biến thiên ta thấy tiếp điểm là $(0;-5)$ và $y'(0)=0$.

Vậy phương trình đường tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là $y =  - 5$

Đáp án : B