Đề bài

Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm ban đầu vật đang ở vị trí biên. Sau đó \(\dfrac{1}{3}\,\,s\) vật không đổi chiều chuyển động và tới vị trí có tốc độ bằng một nửa tốc độ cực đại. Sau đó vật chuyển động thêm \(\dfrac{4}{3}\,\,s\) và đi được quãng đường dài 9 cm. Tốc độ dao động cực đại của vật là

• A. 7,07 cm/s.
• B. 8,16 cm/s.
• C. 14,13 cm/s.
• D. 16,32 cm/s.

Phương pháp giải

Công thức đọc lập với thời gian: \(\dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{v^2}}}{{{v_{\max }}^2}} = 1\)

Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi  = \omega \Delta t\)

Tốc độ cực đại: \({v_{\max }} = \omega A\)

Lời giải của GV Loigiaihay.com

Tại vị trí vật có tốc độ bằng một nửa tốc độ cực đại, ta có công thức độc lập với thời gian:

\(\dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{v^2}}}{{{v_{\max }}^2}} = 1 \Rightarrow \dfrac{{{x^2}}}{{{A^2}}} + {\left( {\dfrac{1}{2}} \right)^2} = 1 \Rightarrow x =  \pm \dfrac{{A\sqrt 3 }}{2}\)

Ta có vòng tròn lượng giác:

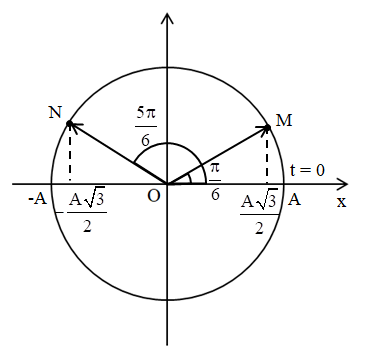
Trường hợp 1: ở thời điểm \(t = \dfrac{1}{3}\,\,s\), vecto quay ở vị trí M, ta có:

\(\Delta \varphi  = \omega \Delta t \Rightarrow \dfrac{\pi }{6} = \omega .\dfrac{1}{3} \Rightarrow \omega  = \dfrac{\pi }{2}\,\,\left( {rad/s} \right)\)

Vật chuyển động thêm \(\dfrac{4}{3}\,\,s\), vecto quay được góc là:

\(\Delta \varphi ' = \omega \Delta t' = \dfrac{\pi }{2}.\dfrac{4}{3} = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\)

→ vecto quay tới vị trí N

Quãng đường vật đi được là:

\(\begin{array}{l}2.\dfrac{{A\sqrt 3 }}{2} = 9\,\,\left( {cm} \right) \Rightarrow A = 3\sqrt 3 \,\,\left( {cm} \right)\\ \Rightarrow {v_{\max }} = \omega A = \dfrac{\pi }{2}.3\sqrt 3  \approx 8,16\,\,\left( {cm/s} \right)\end{array}\)

Trường hợp 2: ở thời điểm \(\dfrac{1}{3}\,\,s\), vecto quay ở vị trí N, ta có:

\(\Delta \varphi  = \omega \Delta t \Rightarrow \dfrac{{5\pi }}{6} = \omega .\dfrac{1}{3} \Rightarrow \omega  = \dfrac{{5\pi }}{2}\,\,\left( {rad/s} \right)\)

Vật chuyển động thêm \(\dfrac{4}{3}\,\,s\), vecto quay được góc là:

\(\Delta \varphi ' = \omega \Delta t' = \dfrac{{5\pi }}{2}.\dfrac{4}{3} = \dfrac{{10\pi }}{3}\,\,\left( {rad} \right) = 2\pi  + \dfrac{{4\pi }}{3}\)

→ vecto quay được 1 vòng và tới vị trí N

Quãng đường vật đi được là:

\(\begin{array}{l}4A + 2A + 2.\left( {A - \dfrac{{A\sqrt 3 }}{2}} \right) = 9\,\,\left( {cm} \right)\\ \Rightarrow A = \dfrac{9}{{8 - \sqrt 3 }} \approx 1,436\,\,\left( {cm} \right)\\ \Rightarrow {v_{\max }} = \omega A = \dfrac{{5\pi }}{2}.1,436 \approx 11,28\,\,\left( {cm/s} \right)\end{array}\)

Đáp án : B