Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
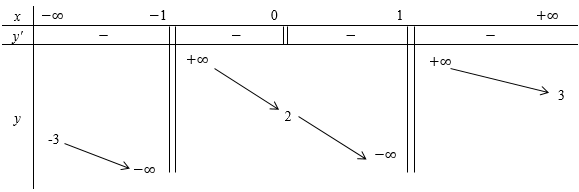
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
-
A.
$m \leqslant - 2$ hoặc $m \geqslant 1$
-
B.
$m \geqslant 1$
-
C.
$m < - 2$ hoặc $m > 1$
-
D.
$m \leqslant - 2$
- Biện luận số nghiệm của phương trình dựa vào số giao điểm của đường thẳng và đường cong vừa vẽ được.
Quan sát BBT ta thấy đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt $ \Leftrightarrow \left[ \begin{gathered}2m + 1 < - 3 \hfill \\ 2m + 1 > 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m < - 2 \hfill \\ m > 1 \hfill \\ \end{gathered} \right.$ .
Đáp án : C
Đường thẳng \(y = - 3\) chỉ cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất 1 điểm \({x_0} \in \left( {0;1} \right)\) nên không thỏa mãn bài toán
(ở nhánh bên trái thì \(y = - 3\) không cắt đồ thị vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 3\), các em có thể hiểu là \(f\left( x \right) = - 3\) thì \(x = - \infty \) nên coi như không có \(x\))
Đường thẳng \(y = 3\) chỉ cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất 1 điểm \({x_1} \in \left( { - 1;0} \right)\) nên không thỏa mãn bài toán
(ở nhánh bên phải thì \(y = 3\) không cắt đồ thị vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 3\), các em có thể hiểu là \(f\left( x \right) = 3\) thì \(x = + \infty \) nên coi như không có \(x\))

Các bài tập cùng chuyên đề


















Danh sách bình luận