Đề bài

Cho  tứ giác $ABCD$, lấy bất kỳ $E \in BD$ . Qua $E$ vẽ $EF$ song song với $AD$( $F$ thuộc $AB$), vẽ $EG$ song song với $DC$($G$ thuộc$BC$). Chọn khẳng định sai.

• A.  $\dfrac{{BE}}{{ED}} = \dfrac{{BG}}{{GC}}$      
• B. $\dfrac{{BF}}{{FA}} = \dfrac{{BG}}{{GC}}$       
• C. $FG{\rm{//}}AC$    
• D. $FG{\rm{//}}AD$

Phương pháp giải

Sử dụng định lý Ta-lét và định lý Ta-lét đảo để suy ra các hệ thức đúng.

Lời giải của GV Loigiaihay.com

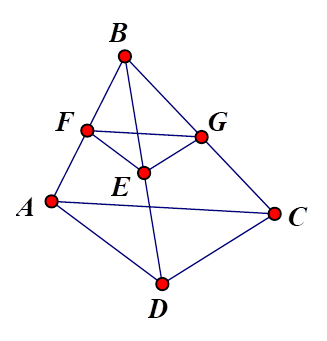
Áp dụng định lí Ta-lét trong $\Delta ABD$ với $EF{\rm{//}}AD$, ta có $\dfrac{{BE}}{{ED}} = \dfrac{{BF}}{{FA}}$. (1)

Áp dụng định lí Ta-lét trong$\Delta BDC$ với $EG{\rm{//}}DC$, ta có $\dfrac{{BE}}{{ED}} = \dfrac{{BG}}{{GC}}$. (2)

Từ (1) và (2) suy ra$\dfrac{{BF}}{{FA}} = \dfrac{{BG}}{{GC}}$, do đó $FG{\rm{//}}AC$(định lí Ta-lét đảo).

Vậy A, B, C đúng, D sai.

Đáp án : D