Đề bài

 Cho hình thang $ABCD$ $\left( {AB{\rm{//}}CD} \right)$ có $BC = 15\,cm$. Điểm $E$ thuộc cạnh $AD$ sao cho $\dfrac{{AE}}{{AD}} = \dfrac{1}{3}$. Qua $E$ kẻ đường thẳng song song với $CD$ , cắt $BC$ ở $F$ . Tính độ dài $BF$ .

• A. \(15\,cm\)       
• B. \(5\,cm\)         
• C. \(10\,cm\)                   
• D. \(7cm\)\(\)

Lời giải của GV Loigiaihay.com

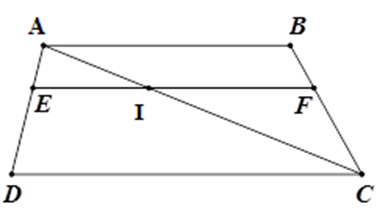
Gọi $I$ là giao điểm của $AC$ và$EF$ .

Xét tam giác \(ACB\) có \(IF{\rm{//}}AB\) nên theo định lý Ta-lét ta có

$\dfrac{{BF}}{{BC}} = \dfrac{{AI}}{{AC}} = \dfrac{{AE}}{{AD}} = \dfrac{1}{3}$ nên

$BF = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\left( {cm} \right)$

Đáp án : B