Đề bài

Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?

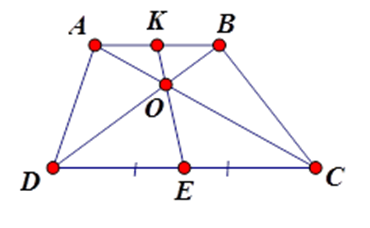
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\)   (II)\(AK = KB\)            

(III) \(\dfrac{{AO}}{{AC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)

• A. \(1\)    
• B. \(2\)    
• C.  \(3\)               
• D. \(4\)

Lời giải của GV Loigiaihay.com

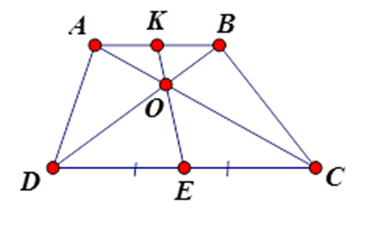
Theo định lý Ta-lét:

Vì \(AK{\rm{//}}EC\) nên \(\dfrac{{AK}}{{EC}} = \dfrac{{OK}}{{OE}}\) và \(KB{\rm{//}}ED\) nên \(\dfrac{{BK}}{{ED}} = \dfrac{{OK}}{{OE}} = \dfrac{{OB}}{{OD}}\) từ đó \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) và \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)

Mà \(EC = ED \Rightarrow AK = KB\) .

Nên (I), (II), (IV) đúng.

Vì \(AB{\rm{//}}DC \Rightarrow \dfrac{{AO}}{{OC}} = \dfrac{{AB}}{{DC}}\)  nên (III) sai.

Đáp án : C