Đề bài

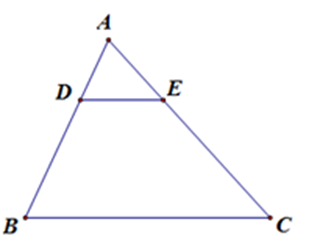
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:

• A. \(20\)                      
• B. \(\dfrac{{18}}{{25}}\)                     
• C. \(50\)                      
• D. \(45\)

Phương pháp giải

Sử dụng định lý Ta-lét tính \(AE\)  từ đó tính \(AC\) .

Lời giải của GV Loigiaihay.com

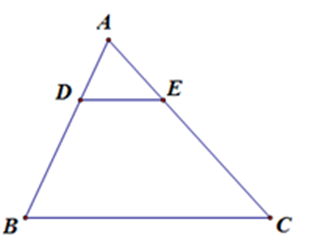
Vì $DE{\rm{//}}BC$, theo định lý Ta-lét ta có \(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{EC}} \Leftrightarrow \dfrac{{12}}{{18}} = \dfrac{{AE}}{{30}}\)\( \Rightarrow EA = \dfrac{{30.12}}{{18}} = 20\,cm\)

Nên \(AC = AE + EC = 50\,cm\)

Đáp án : C