Bài 70 trang 88 SGK Toán 7 tập 2Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB. Quảng cáo
Đề bài Cho \(A, B\) là hai điểm phân biệt và \(d\) là đường trung trực của đoạn thẳng \(AB.\) a) Ta kí hiệu \({P_A}\) là nửa mặt phẳng bờ \(d\) có chứa điểm \(A\) (không kể đường thẳng \(d\)). Gọi \(N\) là một điểm của \({P_A}\) và \(M\) là giao điểm của đường thẳng \(NB\) và \(d.\) Hãy so sánh \(NB\) với \(NM + MA;\) từ đó suy ra \(NA < NB.\) b) Ta kí hiệu \({P_B}\) là nửa mặt phẳng bờ \(d\) có chứa điểm \(B\) (không kể \(d\)). Gọi \(N’\) là một điểm của \({P_B}.\) Chứng minh rằng \(N’B < N’A.\) c) Gọi \(L\) là một điểm sao cho \(LA < LB.\) Hỏi điểm \(L\) nằm ở đâu, trong \({P_A},{P_B}\) hay trên \(d\)? Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Áp dụng tính chất đường trung trực của đoạn thẳng. - Áp dụng bất đẳng thức trong tam giác. Lời giải chi tiết
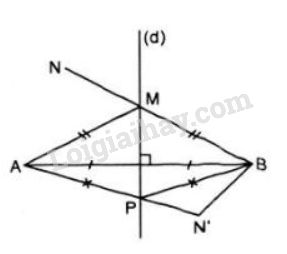
a) - Ta có \(M\) nằm trên đường trung trực của \(AB\) nên \(MA = MB.\) Vì \(M\) nằm giữa đoạn \(NB\) nên: \(NB = NM + MB\) hay \(NB = NM + MA\) (vì \(MB = MA\)) Vậy \(NB = NM + MA\) - Trong \(ΔNMA\) có: \(NA < NM + MA\) (bất đẳng thức tam giác). Vì \(NM + MA = NB\) nên \(NA < NB\) (điều phải chứng minh). b) Nối \(N'A\) cắt \((d)\) tại \(P.\) Vì \(P\) nằm trên đường trung trực của đoạn \(AB\) nên: \(PA = PB\) Ta có: \(N'A = N'P + PA = N'P + PB\) Trong \(ΔN'PB\) ta có: \(N'B < N'P + PB\) Do đó: \(N'B < N'A\) (điều phải chứng minh) c) - Vì \(LA < LB\) nên \(L\) không thuộc đường trung trực \(d.\) - Từ câu b) ta suy ra với điểm \(N'\) bất kì thuộc \(PB\) thì ta có \(N'B < N'A.\) Do đó, để \(LA < LB\) thì \(L\) không thuộc \(P_B.\) - Từ câu a) ta suy ra với điểm \(N\) bất kì thuộc \(PA\) thì ta có \(NA < NB.\) Do đó, để \(LA < LB\) thì \(L\) thuộc \(P_A.\) Loigiaihay.com
|





















Danh sách bình luận