Bài 62 trang 83 SGK Toán 7 tập 2Chứng minh rằng một tam giác Quảng cáo
Đề bài Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Ta chứng mình tam giác cân bằng cách chứng minh hai góc ở đáy bằng nhau. Lời giải chi tiết TH1: Tam giác \(ABC\) vuông tại \(A\) Vì tam giác \(ABC\) vuông tại \(A\) nên \(AB \bot AC\) hay \(BA\) và \(CA\) chính là các đường cao xuất phát từ các đỉnh của hai góc nhọn B và C. Theo đề bài ta có hai chiều cao này bằng nhau \(AB=AC\) nên tam giác \(ABC\) cân tại \(A\) TH2: Tam giác \(ABC\) không có góc vuông.
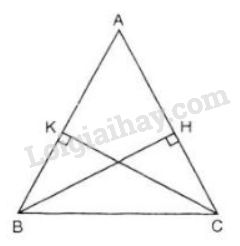
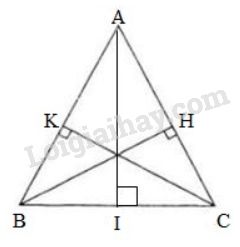
Xét tam giác \(ABC\) có \(BH ⊥ AC\) tại \(H\) và \(CK ⊥ AB\) tại \(K\), biết \(BH=CK.\) Xét hai tam giác vuông \(KBC\) và \(HCB\) có: +) \(BC\) cạnh chung +) \(BH = CK\) (giả thiết) Vậy \({\Delta}KBC = {\Delta}HCB\) (cạnh huyền - cạnh góc vuông) \( \Rightarrow \; \widehat{KBC}= \widehat{HCB}\) (Hai góc tương ứng). \( \Rightarrow ∆ABC\) cân tại \(A\) (điều phải chứng minh). *) Xét \(ΔABC\) có ba đường cao \(BH = CK = AI\)
Theo chứng minh trên ta có: +) Nếu \(BH = CK\) thì \(ΔABC\) cân tại \(A\) \( \Rightarrow AB = AC\) (1) +) Nếu \(AI = BH\) thì \(ΔABC\) cân tại \(C\) \( \Rightarrow CA = CB\) (2) Từ (1) và (2) ta có: \(AB = BC = AC\). Vậy \(ΔABC\) là tam giác đều (điều phải chứng minh).
|