Bài 6 trang 74 Tài liệu dạy – học Toán 9 tập 1

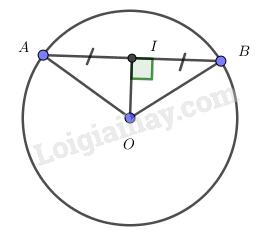
Đề bài

Cho đường tròn tâm O bán kính R = 10 cm. A, B là hai điểm trên đường tròn (O) và I là trung điểm của đoạn thẳng AB.

a) Tính AB nếu OI = 7 cm.

b) Tính OI nếu AB = 14 cm.

Lời giải chi tiết

a) Tính AB nếu OI = 7 cm.

Có A, B là hai điểm trên đường tròn (O) và I là trung điểm của đoạn thẳng AB

\( \Rightarrow OI \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung)

Áp dụng định lý Pythagore vào tam giác OIA vuông tại I:

\(A{I^2} = O{A^2} - O{I^2} = {10^2} - {7^2} = 51\)

\(\Rightarrow AI = \sqrt {51} \)(cm)

Có I là trung điểm của đoạn thẳng AB \( \Rightarrow AB = 2.AI = 2\sqrt {51} \) (cm)

b) Tính OI nếu AB = 14 cm.

Có I là trung điểm của đoạn thẳng AB \( \Rightarrow AI = \dfrac{1}{2}.AB = 7\) (cm)

Áp dụng định lý Pythagore vào tam giác OIA vuông tại I:

\(O{I^2} = O{A^2} - A{I^2} = {10^2} - {7^2} = 51 \)

\(\Rightarrow OI = \sqrt {51} \) (cm)

Loigiaihay.com