Bài 6 trang 148 Tài liệu dạy – học Toán 9 tập 1

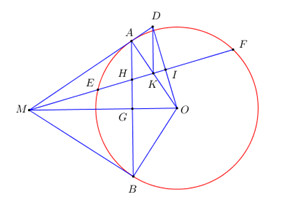
Đề bài

Từ điểm M ở ngoài đường tròn (O ; R) vẽ tiếp tuyến MA, MB và cát tuyến MEF với (O) (A và B là hai tiếp điểm ; ME < MF ; tia MF nằm giữa hai tia MA, MO).

a) Chứng minh rằng OM là trung trực của AB.

b) Gọi I là trung điểm của EF. Đường thẳng MA cắt đường thẳng OI tại D ; OA cắt MI tại K. Chứng minh rằng \(DK \bot MO\).

c) Gọi H là giao điểm của AB với MI. Tính đoạn HI khi tam giác MAB đều và \(OI = \dfrac{R}{2}\).

Lời giải chi tiết

 

a) Ta có : \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).

\(OA = OB = R \Rightarrow O\) thuộc trung trực của \(AB\) .

\( \Rightarrow OM\) là trung trực của \(AB\).

b) Vì I là trung điểm của EF \( \Rightarrow OI \bot EF\) (quan hệ vuông góc giữa đường kính và dây cung)

Xét tam giác ODM có :

\(\left\{ \begin{array}{l}MI \bot OD\\OA \bot MD\\OA \cap MI = K\end{array} \right.\) \( \Rightarrow K\) là trực tâm của \(\Delta ODM \Rightarrow DK \bot OM\).

c) Gọi \(G = OM \cap AB\) \( \Rightarrow G\) là trung điểm của \(AB\).

Do \(\Delta MAB\) đều \( \Rightarrow \) trung tuyến \(MG\) đồng thời là phân giác \( \Rightarrow \angle AMG = \dfrac{1}{2}\angle AMB = \dfrac{1}{2}{.60^0} = {30^0}\).

\( \Rightarrow \angle AOM = {60^0} \) \(\Rightarrow OG = OA.\cos {60^0} = \dfrac{R}{2} = OI\).

 Xét tam giác vuông OHI và tam giác vuông OHG có :

\(\begin{array}{l}OH\,chung\\OI = OG\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow \Delta OHI = \Delta OGI\) (cạnh huyền – cạnh góc vuông)

\( \Rightarrow HI = HG\) (2 cạnh tương ứng).

Xét tam giác vuông OAM có : \(\sin {30^0} = \dfrac{{OA}}{{OM}} \) \(\Rightarrow OM = \dfrac{{OA}}{{\sin {{30}^0}}} = \dfrac{R}{{\dfrac{1}{2}}} = 2R\)

Áp dụng định lí Pytago trong tam giác vuông OAM có \(AM = \sqrt {O{M^2} - O{A^2}}  = \sqrt {{{\left( {2R} \right)}^2} - {R^2}}  = R\sqrt 3 \)

Áp dụng hệ thức lượng trong tam giác vuông OAM có : \(M{A^2} = MO.MG \)

\(\Rightarrow MG = \dfrac{{M{A^2}}}{{MO}} = \dfrac{{3{R^2}}}{{2R}} = \dfrac{{3R}}{2}\).

Áp dụng định lí Pytago trong tam giác vuông OIM có \(I{M^2} = O{M^2} - O{I^2} = {\left( {2R} \right)^2} - {\left( {\dfrac{R}{2}} \right)^2} = \dfrac{{15R}}{4} \)

\(\Rightarrow IM = \dfrac{{R\sqrt {15} }}{2}\)

Xét tam giác vuông MGH và tam giác vuông MOI ta có :

\(\angle OMI\) chung ;

\(\angle MGH = \angle MIO = {90^0}\)

\( \Rightarrow \Delta MGH \sim \Delta MIO\,\,\left( {g.g} \right) \\\Rightarrow \dfrac{{HG}}{{OI}} = \dfrac{{MG}}{{MI}} \\\Rightarrow HG = \dfrac{{OI.MG}}{{MI}} = \dfrac{{\dfrac{R}{2}.\dfrac{{3R}}{2}}}{{\dfrac{{R\sqrt {15} }}{2}}} = \dfrac{{R\sqrt {15} }}{{10}}\)

Vậy \(HI = \dfrac{{R\sqrt {15} }}{{10}}\).

 Loigiaihay.com