Bài 51 trang 127 SGK Toán 8 tập 2Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao h và đáy lần lượt là: Quảng cáo
Video hướng dẫn giải Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao \(h\) và đáy lần lượt là: LG a. Hình vuông cạnh \(a\); Phương pháp giải: Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng. + Diện tích xung quanh hình lăng trụ bằng tích của chu vi đáy và chiều cao. + Diện tích toàn phần hình lăng trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. + Thể tích hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao. Lời giải chi tiết:
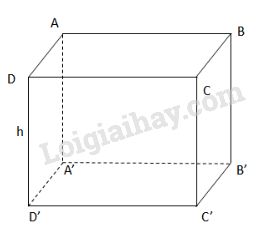
Kí hiệu lăng trụ đứng đã cho như hình bên. p là nửa chu vi đáy và h là chiều cao lăng trụ. Diện tích xung quanh là: \({S_{xq}} = 2p.h = 4.a.{\text{ }}h\) Diện tích một đáy là : \({S_đ} = {a^2}\) Diện tích toàn phần của lăng trụ đứng là : \({S_{tp}} = {S_{xq}} + 2{S_đ} = 4ah + 2{a^2}\) Thể tích lăng trụ : \(V = {S_đ}h = {a^2}.h\) LG b. Tam giác đều cạnh \(a\); Phương pháp giải: Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng. + Diện tích xung quanh hình lăng trụ bằng tích của chu vi đáy và chiều cao. + Diện tích toàn phần hình lăng trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. + Thể tích hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao. Lời giải chi tiết:
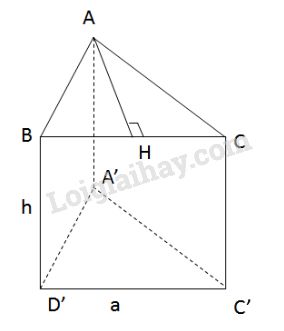
Chiều cao của tam giác đều ABC là: \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\dfrac{a }{ 2}} \right)}^2}} \) \( = \sqrt {\dfrac{{3{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\) Diện tích xung quanh là: \({S_{xq}} = 2p.h = 3a.h\) Diện tích một đáy là: \({S_đ} = \dfrac{1}{2}a.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4}\) Diện tích toàn phần là: \({S_{tp}} = {S_{xq}} + 2{S_đ}=3ah +2.\dfrac{{{a^2}\sqrt 3 }}{4}\)\(\, = 3ah + \dfrac{{{a^2}\sqrt 3 }}{2}\) Thể tích: \(V = {S_đ}.h = \dfrac{{{a^2}\sqrt 3 }}{4}.h = \dfrac{{{a^2}h\sqrt 3 }}{4}\) LG c. Lục giác đều cạnh \(a\); Phương pháp giải: Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng. + Diện tích xung quanh hình lăng trụ bằng tích của chu vi đáy và chiều cao. + Diện tích toàn phần hình lăng trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. + Thể tích hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao. Lời giải chi tiết:
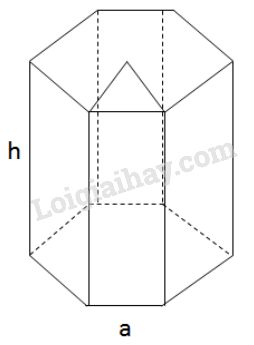
Diện tích xung quanh là: \({S_{xq}}= 2p. h = 6a.h\) Diện tích tam giác đều cạnh a (theo câu b) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\). Do đó diện tích một đáy của lăng trụ là : \({S_đ} = 6.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{2}\) Diện tích toàn phần là: \({S_{tp}} = {S_{xq}} + 2{S_đ}\) \({S_{tp}} = 6ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{2} = 6ah + 3{a^2}\sqrt 3 \)\(\, = 3a\left( {2h + a\sqrt 3 } \right)\) Thể tích tích lăng trụ : \(V = {S_đ}.h = \dfrac{{3{a^2}\sqrt 3 }}{2}.h = \dfrac{{3{a^2}h\sqrt 3 }}{2}\) LG d. Hình thang cân, đáy lớn là \(2a\), các cạnh còn lại bằng \(a\); Phương pháp giải: Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng. + Diện tích xung quanh hình lăng trụ bằng tích của chu vi đáy và chiều cao. + Diện tích toàn phần hình lăng trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. + Thể tích hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao. Lời giải chi tiết:
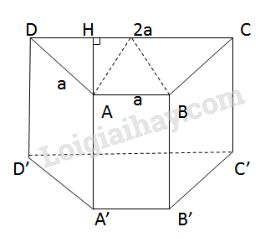
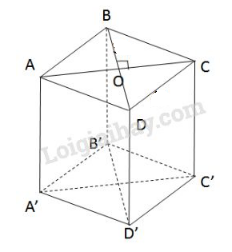
Diện tích xung quanh : \({S_{xq}}= 2ph = (2a + a +a +a). h \)\(\,= 5ah\). Chiều cao hình thang cũng chính là chiều cao tam giác đều cạnh \(a\). \(AH = \dfrac{{a\sqrt 3 }}{2}\) (theo câu b) Diện tích một đáy hình lăng trụ là: \({S_đ} = \dfrac{{\left( {2a + a} \right).AH}}{2} \)\(\,= \dfrac{{3a}}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{3{a^2}\sqrt 3 }}{4}\) Diện tích toàn phần là: \({S_{tp}} = {S_{xq}} + 2{S_đ} = 5ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{4} \)\(\,= 5ah + \dfrac{{3{a^2}\sqrt 3 }}{2}\) Thể tích hình lăng trụ: \(V = S.h = \dfrac{{3{a^2}\sqrt 3 }}{4}.h = \dfrac{{3{a^2}h\sqrt 3 }}{4}\) LG e. Hình thoi có hai đường chéo là \(6a\) và \(8a\). Phương pháp giải: Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng. + Diện tích xung quanh hình lăng trụ bằng tích của chu vi đáy và chiều cao. + Diện tích toàn phần hình lăng trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. + Thể tích hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao. Lời giải chi tiết: Vì hai đường chéo \(BD=6a, AC=8a\) nên \(OB=3a, OC=4a.\) Cạnh của hình thoi: \(BC = \sqrt {O{B^2} + O{C^2}} \) \(= \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} \) \(= \sqrt {25{a^2}} = 5a\) Diện tích xung quanh lăng trụ: \(S_{xq}= 2ph = 4.5a.h = 20ah\) Diện tích một đáy của lăng trụ: \({S_đ} = \dfrac{1}{2}.6a.8a = 24{a^2}\) Diện tích toàn phần: \({S_{tp}} = {S_{xq}} + 2{S_đ} \)\(\,= 20ah + 2.24a^2 = 20ah + 48{a^2}\) Thể tích lăng trụ: \(V = Sh =24{a^2}.h\) Loigiaihay.com
|




















Danh sách bình luận