Bài 43 trang 132 SGK Toán 8 tập 1Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Quảng cáo
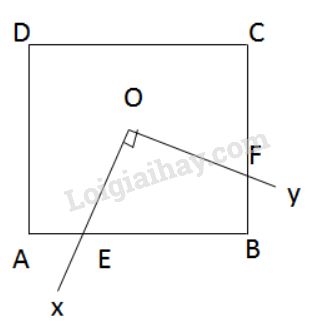
Đề bài Cho hình vuông \(ABCD\) có tâm đối xứng \(O\), cạnh \(a.\) Một góc vuông \(xOy\) có tia \(Ox\) cắt cạnh \(AB\) tại \(E\), tia \(Oy\) cắt cạnh \(BC\) tại \(F\) (h.\(161\))
Tính diện tích tứ giác \(OEBF.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng tính chất hình vuông, công thức tính diện tích tứ giác có hai đường chéo vuông góc; diện tích tam giác vuông, tam giác thường. Lời giải chi tiết
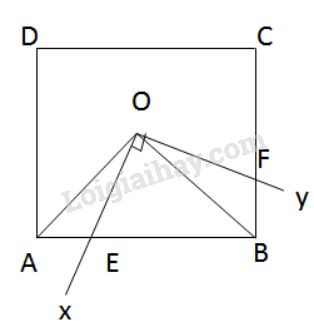
Nối \(OA, OB\). Do \(ABCD\) là hình vuông nên \(O\) là trung điểm của \(AC,BD\) và \(\widehat{AOB}=90^0\) Ta có: \(\widehat {AOE} + \widehat {BOE}=\widehat{AOB}=90^0\) \(\widehat{FOB}+\widehat{EOB}=\widehat{xOy}=90^0\) Nên \(\widehat {AOE} = \widehat {BOF}\) (cùng phụ với \(\widehat {BOE}\)) Xét \(\Delta AOE\) và \(\Delta BOF\) có: +) \(\widehat {AOE} = \widehat {BOF}\) (chứng minh trên) +) \(OA = OB\) (\(O\) là tâm đối xứng của hình vuông) +) \(\widehat {OAE} = \widehat {OBF} = {45^0}\) (tính chất hình vuông) \( \Rightarrow ∆AOE = ∆BOF\, (g.c.g) \) \( \Rightarrow {S_{AOE}} = {S_{BOF}}\) Do đó \({S_{OEBF}} = {S_{OEB}} + {S_{OBF}} \)\(= {S_{OEB}} + {S_{OAE}} = {S_{OAB}}\) \({S_{OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.\dfrac{1}{2}AC.\dfrac{1}{2}BD\)\(\, = \dfrac{1}{4}.\left( {\dfrac{1}{2}AC.BD} \right) = \dfrac{1}{4}{S_{ABCD}}\) Vậy \({S_{OEBF}} =\dfrac{1}{4}{S_{ABCD}}\) \( = \dfrac{1}{4}{a^2}\) Loigiaihay.com
|




















Danh sách bình luận