Bài 33 trang 70 SGK Toán 7 tập 2

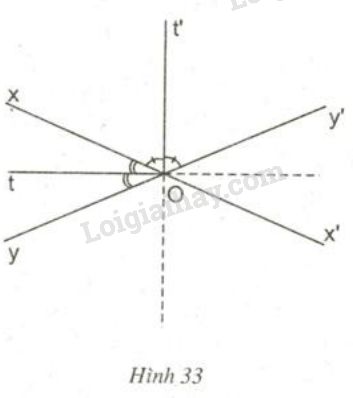
Đề bài

Cho hai đường thẳng \(xx’, yy’\) cắt nhau tại \(O\) (h. 33).

a) Chứng minh rằng hai tia phân giác \(Ot, Ot’\) của một cặp góc kề bù tạo thành một góc vuông.

b) Chứng minh rằng: Nếu \(M\) thuộc đường thẳng \( Ot\) hoặc thuộc đường thẳng \(Ot’\) thì \(M\) cách đều hai đường thẳng \(xx’\) và \( yy’.\)

c) Chứng minh rằng: Nếu \(M\) cách đều hai đường thẳng \(xx’, yy’\) thì \(M\) thuộc đường thẳng \(Ot\) hoặc thuộc đường thẳng \(Ot’\).

d) Khi \(M ≡ O\) thì khoảng cách từ \(M\) đến \(xx’\) và \(yy’\) bằng bao nhiêu ?

e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau \(xx’, yy’.\)

Lời giải chi tiết

a) Vì \(Ot\) là tia phân giác của \(\widehat{xOy}\) 

nên \(\widehat{yOt} = \widehat{xOt} = \dfrac{1}{2}\widehat{xOy}\)

\(Ot'\) là tia phân giác của \(\widehat{xOy'}\)

nên \(\widehat{xOt'} = \widehat{y'Ot'} = \dfrac{1}{2}\widehat{xOy'}\)

\( \Rightarrow\widehat{xOt} + \widehat{xOt'} = \dfrac{1}{2}\widehat{xOy} + \dfrac{1}{2}\widehat{xOy'}\)\(\,=\dfrac{1}{2}\left( \widehat{xOy}+ \widehat{xOy'}\right)\)

Mà \(\widehat{xOy}\) + \(\widehat{xOy'}=  180^o\)  (\(2\) góc kề bù)

\( \Rightarrow\)  \(\widehat{xOt}\) + \(\widehat{xOt'}= \dfrac{1}{2}.{180^o} = {90^o}\)

Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông.

b) Nếu \(M\) thuộc \(Ot\) hoặc \(Ot'\) thì \(M\) cách đều hai đường thẳng \(xx'\) và \(yy'.\)

Thật vậy, giả sử \(M \in  Ot.\)

Do \(Ot\) là phân giác của \(\widehat{xOy}\) nên \(M\) cách đều \(Ox, Oy\) (Theo định lí 1)

\( \Rightarrow\) \(M\) cách đều \(xx',yy'\)

Nếu \(M \in  Ot'\)

Do \(Ot'\) là phân giác của \(\widehat{xOy'}\) nên \(M\) cách đều \(Ox, Oy'\) (Theo định lí 1)

\( \Rightarrow\) \(M\) cách đều \(xx',yy'\) 

\( \Rightarrow\) \(M\) thuộc \(Ot\) hoặc \(Ot'\) thì \(M\) cách đều hai đường thẳng \(xx'\) và \(yy'.\)

c) Nếu \(M\) cách đều hai đường thẳng \(xx', yy'\) và \(M\) luôn nằm trong một góc trong bốn góc \(\widehat{xOy}\), \(\widehat{xOy'}\), \(\widehat{x'Oy'}\),  \(\widehat{x'Oy}\) thì \(M\) phải thuộc phân giác của góc ấy tức \(M\) phải thuộc đường thẳng \(Ot\) hoặc đường thẳng \(Ot'\).

Thật vậy:

M cách đều hai đường thẳng \(xx’\) và \(yy’ \) nên theo định lý 2 ta có:

+ Nếu M thuộc miền trong góc \(xOy ⇒ M\) thuộc tia \(Ot.\)

+ Nếu M thuộc miền trong góc \(xOy’ ⇒ M\) thuộc tia \(Ot’.\)

+ Nếu M thuộc miền trong góc \(y’Ox’ ⇒ M\) thuộc tia đối của tia \(Ot.\)

+ Nếu M thuộc miền trong góc \(x’Oy ⇒ M\) thuộc tia đối của tia \(Ot’ .\)

d) Khi \(M ≡ O\) thì khoảng cách từ \(M\) đến \(xx', yy'\) bằng \(0\). 

e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau \(xx', yy'\) thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.

Loigiaihay.com