Bài 23 trang 83 SGK Toán 6 tập 2

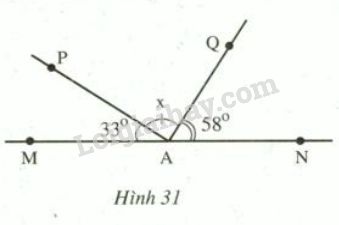
Đề bài

Hình 31 cho biết  hai tia \(AM\) và \(AN\) đối nhau,\(\widehat{MAP}= 33^{0} , \widehat{NAQ}= 58^{0},\) tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP .\) Hãy tính số đo \(x\) của \(\widehat{PAQ}\) 

Lời giải chi tiết

Vì \(AM\) và \(AN\) là hai tia đối nhau nên \(\widehat{MAP}\) và \(\widehat{PAN}\) là hai góc kề bù.

Do đó, \(\widehat{MAP}+\widehat{PAN}=180^0\) 

Suy ra \(\widehat{PAN}=180^0-\widehat{MAP}\)\(={180^0} - {33^0} = {147^0}\)

Vì tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP\)

Suy ra \(\widehat{PAN}=\widehat{PAQ}+\widehat{QAN}\)

Hay \(147^0= x + 58^0 \)

Nên \(x = 147^0-58^0=89^0\)

Vậy \(\widehat{PAQ}=89^0\) 

Loigiaihay.com