Bài 19 trang 112 Tài liệu dạy – học Toán 9 tập 2

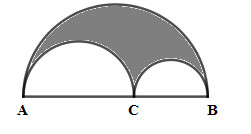
Đề bài

Cho nửa đường tròn (O ; 10 cm) đường kính AB. Vẽ hai nửa đường tròn đường kính CA, CB ở trong nửa đường tròn (O), biết CA = 6 cm, CB = 4 cm và \(\pi  = 3,14\). Hãy tính diện tích phần tô đen.

 

Lời giải chi tiết

Diện tích nửa hình tròn đường kính AB là \({S_1} = \dfrac{1}{2}\pi {\left( {\dfrac{{AB}}{2}} \right)^2} = \dfrac{1}{2}\pi {.5^2} = \dfrac{{25}}{2}\pi \,\,\,\left( {c{m^2}} \right)\)

Diện tích nửa hình tròn đường kính AC là: \({S_2} = \dfrac{1}{2}\pi {\left( {\dfrac{{AC}}{2}} \right)^2} = \dfrac{1}{2}\pi {.3^2} = \dfrac{9}{2}\pi \,\,\left( {c{m^2}} \right)\)

Diện tích nửa hình tròn đường kính BC là: \({S_2} = \dfrac{1}{2}\pi {\left( {\dfrac{{BC}}{2}} \right)^2} = \dfrac{1}{2}\pi {.2^2} = 2\pi \,\,\left( {c{m^2}} \right)\)

Vậy diện tích phần tô đen là \(S = {S_1} - \left( {{S_2} + {S_3}} \right) = \dfrac{{25}}{2}\pi  - \left( {\dfrac{9}{2}\pi  + 2\pi } \right)\)\(\, = 6\pi  \approx 18,84\,\,\left( {c{m^2}} \right)\).

 Loigiaihay.com