Bài 14 trang 101 SGK Hình học 12Trong không gian cho ba điểm A, B, C. Xác định điểm G sao cho Quảng cáo
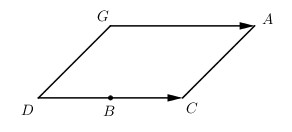
Video hướng dẫn giải Trong không gian cho ba điểm \(A, B, C\). LG a Xác định điểm \(G\) sao cho \(\overrightarrow {GA} + 2\overrightarrow {GB} - 2\overrightarrow {GC} = 0.\) Phương pháp giải: Biến đổi đẳng thức vector trong câu a) theo những điểm cố định và suy ra vị trí của điểm G. Lời giải chi tiết: Ta có \(\begin{array}{l} Gọi \(D\) là điểm mà \(\overrightarrow {DC} = 2\overrightarrow {BC} \) tức là điểm \(B\) là trung điểm của \(CD\) \( \Rightarrow \overrightarrow {GA} = \overrightarrow {DC} \) Vậy \(G\) là đỉnh thứ tư của hình bình hành \(ACDG\).
LG b Tìm tập hợp các điểm \(M\) sao cho \(MA^2 + 2MB^2 - 2MC^2 = k^2\), với \(k\) là hằng số. Phương pháp giải: Sử dụng công thức ba điểm, chèn điểm G vào tất cả các vector \(\overrightarrow {MA} ;\overrightarrow {MB} ;\overrightarrow {MC} \), biến đổi và kết luận. Lời giải chi tiết: Gọi \(G\) là điểm trong câu a): \(\overrightarrow {GA} + 2\overrightarrow {GB} - 2\overrightarrow {GC} = \overrightarrow 0 \). Ta có: \(M{A^2} = {\overrightarrow {MA} ^2}= {(\overrightarrow {MG} + \overrightarrow {GA} )^2}\) \(= M{G^2} + G{A^2} + 2\overrightarrow {MG} .\overrightarrow {GA} \); \(M{B^2} = {\overrightarrow {MB} ^2} = {(\overrightarrow {MG} + \overrightarrow {GB} )^2}\) \(= M{G^2} + G{B^2} + 2\overrightarrow {MG} .\overrightarrow {GB} \); \(M{C^2} = {\overrightarrow {MC} ^2} = {(\overrightarrow {MG} + \overrightarrow {GC} )^2} \) \(= M{G^2} + G{C^2} + 2\overrightarrow {MG} .\overrightarrow {GC} \). Từ đó \(MA^2 +2 MB^2 -2 MC^2 = k^2\) \( \Leftrightarrow M{G^2} + G{A^2} + 2G{B^2} - 2G{C^2} \) \(+ 2\overrightarrow {MG} (\overrightarrow {GA} + 2\overrightarrow {GB} - 2\overrightarrow {GC} ) = {k^2}\) \( \Leftrightarrow M{G^2} = {k^2} - (G{A^2} + 2G{B^2} - 2G{C^2})\) (Vì \(\overrightarrow {GA} + 2\overrightarrow {GB} - 2\overrightarrow {GC} = \overrightarrow 0 \)). Do vậy: Nếu \(k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 > 0\) thì tập hợp các điểm M là mặt cầu tâm G bán kính r. Nếu \(k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 =0\) thì tập hợp M chính là điểm G. Nếu \(k^2 - (GA^2 + 2GB^2 - 2GC^2) = r^2 < 0\) thì tập hợp các điểm M chính là tập rỗng. Loigiaihay.com
|