Kiểm tra giữa học kì II trang 30Viết tiếp vào chỗ chấm cho thích hợp: Trong số 5 216 604. Viết phân số thích hợp vào chỗ chấm. Ba người bốc vác gạo từ kho ra xe tải. Người đầu tiên bốc vác được 1/5 tấn gạo. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
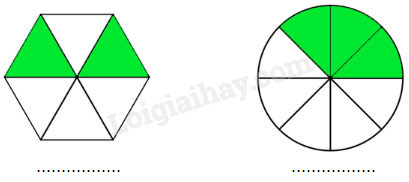
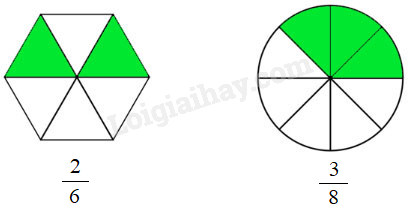
Bài 1 Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây vào chỗ chấm:
Phương pháp giải: Quan sát hình vẽ, tìm số được tô màu và tổng số ô. Phân số chỉ phần đã tô màu có tử số là số ô được tô màu và mẫu số là tổng số ô. Lời giải chi tiết:
Bài 2 Viết tiếp vào chỗ chấm cho thích hợp: Trong số 5 216 604: a) Chữ số 2 thuộc hàng …… lớp …… b) Chữ số 5 thuộc hàng …… lớp …… Phương pháp giải: - Các chữ số từ phải sang trái lần lượt thuộc hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, hàng chục nghìn, hàng trăm nghìn ... - Áp dụng lý thuyết về lớp: + Lớp đơn vị gồm hàng đơn vị, hàng chục, hàng trăm. + Lớp nghìn gồm hàng nghìn, hàng chục nghìn, hàng trăm nghìn. + Lớp triệu gồm hàng triệu, hàng chục triệu, hàng chục triệu. Lời giải chi tiết: Trong số 5 216 604: a) Chữ số 2 thuộc hàng trăm nghìn, lớp nghìn. b) Chữ số 5 thuộc hàng triệu, lớp triệu. Bài 3 Khoanh vào chữ đặt trước câu trả lời đúng: Phân số dưới đây bằng phân số \(\dfrac{2}{7}\) là: A. \(\dfrac{4}{{21}}\) B. \(\dfrac{6}{{21}}\) C. \(\dfrac{3}{9}\) D. \(\dfrac{1}{4}\) Phương pháp giải: Áp dụng tính chất cơ bản của phân số: • Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho. • Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho. Lời giải chi tiết: Ta có: \(\dfrac{2}{7} = \dfrac{{2 \times 3}}{{7 \times 3}} = \dfrac{6}{{21}}\) ; \(\dfrac{3}{9} =\dfrac{3:3}{9:3} =\dfrac{1}{3} \) Các phân số \(\dfrac{4}{{21}}\;;\;\dfrac{1}{4}\) là các phân số tối giản. Vậy trong các phân số đã cho, phân số bằng phân số \(\dfrac{2}{7}\) là \(\dfrac{6}{{21}}\). Chọn B. Bài 4 Viết số thích hợp vào chỗ chấm: a) 700 000cm2 = …….. m2 b) 27m2 95cm2 = …….. cm2 Phương pháp giải: Áp dụng tính chất : 1m2 = 10 000cm2. Lời giải chi tiết: a) 700 000cm2 = 70m2 b) 27m2 95cm2 = 270095cm2 Bài 5 Viết phân số thích hợp vào chỗ chấm: Trong các phân số \(\dfrac{1}{3};\dfrac{7}{6};\dfrac{{15}}{{12}};\dfrac{5}{5};\dfrac{{16}}{{17}};\dfrac{{18}}{{18}}\), các phân số lớn hơn \(1\) là: ..... Phương pháp giải: Các phân số có tử số lớn hơn mẫu số thì lớn hơn \(1\). Lời giải chi tiết: Các phân số có tử số lớn hơn mẫu số thì lớn hơn \(1\). Do đó trong các phân số đã cho, phân số lớn hơn \(1\) là: \(\dfrac{7}{6}\,\,;\,\,\dfrac{{15}}{{12}}.\) Bài 6 Quy đồng mẫu số các phân số: a) \(\dfrac{4}{7}\) và \(\dfrac{3}{5}\) b) \(\dfrac{7}{4}\) và \(\dfrac{9}{8}\) Phương pháp giải: * Khi quy đồng mẫu số hai phân số có thể làm như sau: - Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai. - Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất. * Nếu mẫu số của một trong hai phân số chia hết cho mẫu số của phân số còn lại thì ta có thể quy đồng mẫu số hai phân số như sau: - Lấy mẫu số chung là mẫu số lớn hơn. - Tìm thừa số phụ bằng cách lấy mẫu số lớn hơn chia cho mẫu số nhỏ hơn. - Nhân cả tử số và mẫu số của phân số có mẫu số nhỏ hơn với thừa số phụ tương ứng. - Giữ nguyên phân số có mẫu số lớn hơn. Lời giải chi tiết: a) Ta có: \(\dfrac{4}{7} = \dfrac{{4 \times 5}}{{7 \times 5}} = \dfrac{{20}}{{35}};\) \(\dfrac{3}{5} = \dfrac{{3 \times 7}}{{5 \times 7}} = \dfrac{{21}}{{35}}\) Vậy quy đồng mẫu số của \(\dfrac{4}{7}\) và \(\dfrac{3}{5}\) được \(\dfrac{{20}}{{35}}\) và \(\dfrac{{21}}{{35}}\). b) Ta có: \(\dfrac{7}{4} = \dfrac{{7 \times 2}}{{4 \times 2}} = \dfrac{{14}}{8};\) Giữ nguyên phân số \(\dfrac{9}{8}\). Vậy quy đồng mẫu số của \(\dfrac{7}{4}\) và \(\dfrac{9}{8}\) được \(\dfrac{{14}}{8}\) và \(\dfrac{9}{8}\). Bài 7 Đúng ghi Đ, sai ghi S:
Phương pháp giải: Áp dụng các dấu hiệu chia hết cho 2; 5; 9; 3: - Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2. - Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5. - Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5. - Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9. - Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3. Lời giải chi tiết:
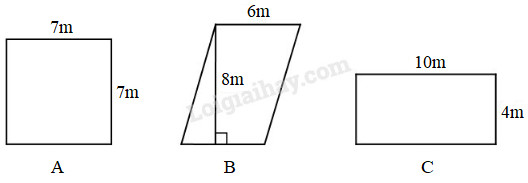
Bài 8 Khoanh vào chữ đặt dưới hình có diện tích lớn nhất:
Phương pháp giải: Tính diện tích các hình theo quy tắc: - Muốn tính diện tích hình vuông ta lấy cạnh nhân với cạnh. - Muốn tính diện tích hình bình hành ta lấy độ dài đáy nhân với chiều cao tương ứng (cùng một đơn vị đo). - Muốn tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo). Lời giải chi tiết: Diện tích hình vuông A là: \(7 \times 7 = 49\,\,({m^2})\) Diện tích hình bình hành B là: \(6 \times 8 = 48\,\,({m^2})\) Diện tích hình chữ nhật C là: \(10 \times 4 = 40\,\,({m^2})\) Ta có: \(40{m^2} < 48{m^2} < 49{m^2}\). Vậy hình có diện tích lớn nhất là hình vuông A. Câu 9 Tìm hai phân số vừa lớn hơn \(\dfrac{1}{7}\) vừa bé hơn \(\dfrac{1}{2}\). Phương pháp giải: Cách 1 : Áp dụng cách so sánh hai phân số có cùng tử số. Cách 2: Quy đồng hai phân số \(\dfrac{1}{7}\) và \(\dfrac{1}{2}\) với mẫu số chung là \(14\) hoặc \(28\) hoặc \(42\), … rồi tìm các phân số thỏa mãn điều kiện đề bài. Lời giải chi tiết: Cách 1 : Ta có : \(\dfrac{1}{{7}} < \dfrac{1}{{6}} < \dfrac{1}{{5}} < \dfrac{1}{{4}} < \dfrac{1}{{3}}< \dfrac{1}{{2}}\) Vậy ta có thể chọn hai phân số vừa lớn hơn \(\dfrac{1}{7}\) vừa bé hơn \(\dfrac{1}{2}\) là \(\dfrac{1}{{5}}\,;\,\,\dfrac{1}{{4}}\) hoặc \(\dfrac{1}{{6}}\,;\,\,\dfrac{1}{3}\) ; ... Cách 2 : Ta có: \(\dfrac{1}{7} = \dfrac{{1 \times 2}}{{7 \times 2}} = \dfrac{2}{{14}};\) \(\dfrac{1}{2} = \dfrac{{1 \times 7}}{{2 \times 7}} = \dfrac{7}{{14}}\) Lại có: \(\dfrac{2}{{14}} < \dfrac{3}{{14}} < \dfrac{4}{{14}} < \dfrac{5}{{14}}< \dfrac{6}{{14}} < \dfrac{7}{{14}}\) . Vậy ta có thể chọn hai phân số vừa lớn hơn \(\dfrac{1}{7}\) vừa bé hơn \(\dfrac{1}{2}\) là \(\dfrac{3}{{14}}\,;\,\,\dfrac{4}{{14}}\) hoặc \(\dfrac{5}{{14}}\,;\,\,\dfrac{6}{14}\) ; ... Lưu ý : Bài tập này có nhiều đáp án đúng khác nhau, học sinh có thể tùy chọn các đáp án thỏa mãn yêu cầu bài toán. Bài 10 Ba người bốc vác gạo từ kho ra xe tải. Người đầu tiên bốc vác được \(\dfrac{1}{5}\) tấn gạo, người thứ hai bốc vác được số tấn gạo gấp đôi người thứ nhất, người thứ ba bốc vác được số tấn gạo bằng mức trung bình của hai người đầu. Hỏi cả ba người bốc vác được bao nhiêu tạ gạo? Phương pháp giải: Đổi 1 tấn = 10 tạ. - Tìm số gạo người thứ nhất bốc vác được ta lấy 10 tạ nhân với \(\dfrac{1}{5}\). - Tìm số gạo người thứ hai bốc vác được ta lấy số gạo người thứ nhất bốc vác được nhân với 2. - Tìm số gạo người thứ ba bốc vác được ta lấy tổng số gạo người thứ nhất và người thứ hai bốc vác được chia cho 2. - Tìm số gạo ba người bốc vác được ta lấy số gạo người thứ nhất bốc vác được cộng với số gạo người thứ hai bốc vác được rồi cộng với số gạo người thứ ba bốc vác được. Lời giải chi tiết: Đổi: \(1\) tấn \(= 10\) tạ. Người thứ nhất bốc vác được số tạ gạo là: \(10 \times \dfrac{1}{5} = 2\) (tạ) Người thứ hai bốc vác được số tạ gạo là: \(2 \times 2 = 4\) (tạ) Người thứ ba bốc vác được số tạ gạo là: \((2 + 4):2 = 3\) (tạ) Cả ba người bốc vác được số tạ gạo là: \(2 + 4 + 3 = 9\) (tạ) Đáp số: \(9\) tạ. Loigiaihay.com
Quảng cáo
|