Bài 1 trang 112 Vở bài tập toán 7 tập 2Giải bài 1 trang 112 VBT toán 7 tập 2. Hình 61 cho biết a//b, góc C bằng 44 độ, góc D bằng 132 độ. Tính số đo góc COD... Quảng cáo
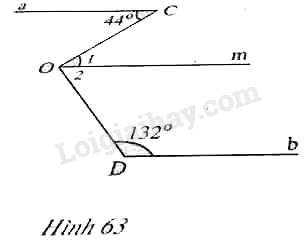
Đề bài (H.63) (Hình \(61\) SGK) Cho biết \(a//b\), \(\widehat {C} = {44^o}\), \(\widehat {D} = {132^o}\). Tính số đo góc \(COD\). (Hướng dẫn: Vẽ đường thẳng song song với đường thẳng \(a\) và đi qua điểm \(O\)).
Phương pháp giải - Xem chi tiết - Vẽ đường thẳng \(m\) đi qua \(O\) và song song với \(a\). - Áp dụng tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau, hai góc trong cùng phía bù nhau. Lời giải chi tiết Kẻ tia \(Om//a\) thì \(\widehat{O_1}=\widehat{C}=44^{\circ}\) (hai góc so le trong) \(Om//a\) mà \(a//b\) nên \(Om//b\). Do đó \(\widehat {O_2} + \widehat{D}= {180^o}\) (hai góc trong cùng phía bù nhau) Suy ra: \(\widehat {O_2} = {180^o} - \widehat{D} = {180^o}-{132^o} = {48^o}\) Vậy \(\widehat {COD} = \widehat {O_1} + \widehat {O_2} ={44^o} + {48^o} = {92^o}\). Lưu ý : Ngoài cách giải theo hướng dẫn của SGK, ta còn có thể giải như sau: (h.64)
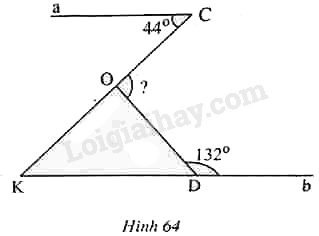
Gọi \(K\) là giao điểm của \(CO\) và \(b\). \(a//b\) nên \(\widehat{K}=\widehat{C}=44^{\circ}\) (hai góc so le trong) \(\widehat{ODK}\) kề bù với \(\widehat{D}\) nên \(\widehat{ODK}=180^{\circ}-\widehat{D}\) =\(180^{\circ}-132^{\circ}=48^{\circ}\) \(\widehat{COD}\) là góc ngoài của \(\Delta OKD\) nên \(\widehat{COD}\) = \(\widehat{K} + \widehat{ODK}\) \(={44^o} + {48^o} = {92^o}\). Loigiaihay.com
Quảng cáo
|