Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 4 - Đại số 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 4 - Đại số 9 Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
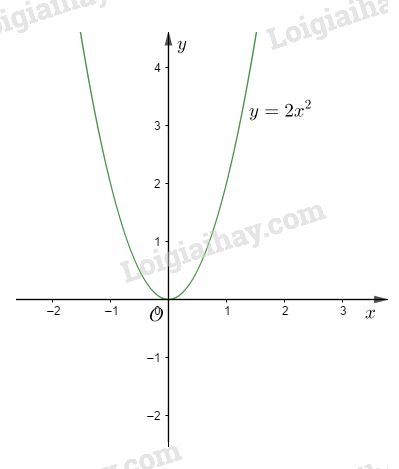
Đề bài Bài 1: Cho đồ thị hai hàm số \(y = {x^2}\) (P) và \(y = 2x \) (d). Tìm tọa độ giao điểm của (P) và (d). Bài 2: Cho hàm số \(y = - {1 \over 4}{x^2}.\) Biết rằng điểm \(M(m; − 1)\) thuộc đồ thị của hàm số. Tìm m. Bài 3: a) Vẽ đồ thị của hàm số \(y = 2{x^2}.\) b) Với giá trị nào của m thì đường thẳng \(y = m\) không cắt đồ thị của hàm số \(y = 2{x^2}.\) LG bài 1 Phương pháp giải: Giải phương trình hoành độ giao điểm tìm được x Thế vào (d) hoặc (P) ta tìm được y =>Tọa độ các giao điểm Lời giải chi tiết: Bài 1: Phương trình hoành độ giao điểm của (P) và (d) : \({x^2} = 2x \Leftrightarrow {x^2} - 2x = 0 \) \(\Leftrightarrow x\left( {x - 2} \right) = 0 \) \(\Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.\) Ta có các giao điểm : \(O(0; 0)\) và \(M(2; 4)\). LG bài 2 Phương pháp giải: Thế tọa độ của M vào hàm số ta tìm được m Lời giải chi tiết: Bài 2: \(M(m; − 1)\) thuộc đồ thị nên \( - 1 = - {1 \over 4}{m^2} \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2.\) LG bài 3 Phương pháp giải: a. Các bước vẽ đồ thị: +Tìm tập xác định của hàm số. +Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y. +Vẽ đồ thị và kết luận. b. a>0 nên đồ thị (P) của hàm số \(y = 2{x^2}\) nằm phía trên của trục \(Ox\) Mà đường thẳng d song song với trục Ox ta suy ra giá trị của m Lời giải chi tiết: Bài 3: a) Bảng giá trị :
Đồ thị của hàm số là parabol có đỉnh là O và nhận trục Oy làm trục đối xứng. b) Đồ thị (P) của hàm số \(y = 2{x^2}\) nằm phía trên của trục \(Ox\). Đường thẳng (d): \(y = m\) là đường thẳng song song với trục \(Ox\). Vậy \(m < 0\) thì (d) và (P) không cắt nhau. Loigiaihay.com
Quảng cáo
|