Cho đường tròn $(O;R)$ đường kính $AB$. Vẽ dây $AC$ sao cho \(\widehat {ABC} = 30^\circ \) . Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM = R$ .
Chọn khẳng định đúng?
-
A.
$MC$ là tiếp tuyến của $(O;R)$
-
B.
$MC$ là cát tuyến của $(O;R)$
-
C.
$MC \bot BC$
-
D.
$MC \bot AC$
Đáp án : A
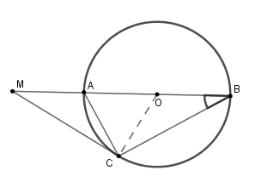
Tam giác $OBC$ cân tại $O$ có \(\widehat {ABC} = 30^\circ \) suy ra $\widehat {AOC} = 60^\circ $ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác $OCA$ là tam giác đều suy ra \(AC = AO = AM = R.\) \( \Rightarrow \widehat {OCM} = {90^ \circ } \Rightarrow MC\) là tiếp tuyến của \((O;R).\)
Các bài tập cùng chuyên đề
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.

















