Cho parabol $\left( P \right):y = {x^2}$ và $d:y = 2x + 3.$
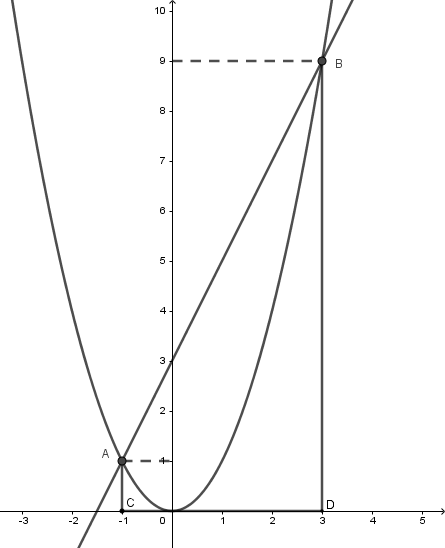
Với giao điểm $A,B$ của $\left( P \right)$ và $d$ ở câu trước . Gọi $C,D$ lần lượt là hình chiếu vuông góc của $A,B$ lên $Ox$. Tính diện tích tứ giác ${\rm{ABDC}}$.
-
A.
${S_{ABDC}} = 20\,\,$(đvdt)
-
B.
${S_{ABDC}} = 40\,$(đvdt)
-
C.
${S_{ABDC}} = 10\,\,$(đvdt)
-
D.
${S_{ABDC}} = 30\,\,$(đvdt)
Đáp án : A
+) Vẽ hình trên cùng một hệ trục tọa độ
+) Xác định tọa độ $C,D$
+) Tính diện tích hình thang vuông ${\rm{ABCD}}$. Sử dụng công thức tính độ dài $A\left( {{x_A};{y_A}} \right);B\left( {{x_B};{y_B}} \right) \Rightarrow AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} $
Ta có $A\left( { - 1;1} \right);B\left( {3;9} \right)$ nên $C\left( { - 1;0} \right);D\left( {3;0} \right)$
$ \Rightarrow AC = \sqrt {{0^2} + {{\left( { - 1} \right)}^2}} = 1;$
$DC = 4;BD = \sqrt {{0^2} + {9^2}} = 9.$
Vì $AC \bot BC;BD \bot BC \Rightarrow ABDC$ là hình thang vuông nên ${S_{ABDC}} = \dfrac{{\left( {AC + BD} \right).DC}}{2} = 20$ (đvdt)
Các bài tập cùng chuyên đề
Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$$\left( {a \ne 0} \right)$ tiếp xúc với nhau khi phương trình $a{x^2} = mx + n$ có
Chọn khẳng định đúng. Nếu phương trình $a{x^2} = mx + n$ vô nghiệm thì đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
Tìm tham số $m$ để đường thẳng $d:y = \dfrac{1}{2}x + m$ tiếp xúc với parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
Tìm tham số $m$ để đường thẳng $d:y = 2x + m$ và parabol $\left( P \right):y = 2{x^2}$ không có điểm chung
Tìm tham số $m$ để đường thẳng $d:y = mx + m + 1$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm bên trái trục tung.
Tìm tham số $m$ để đường thẳng $d:y = \left( {m - 2} \right)x + 3m$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt nằm hai phía của trục tung.
Có bao nhiêu giá trị của tham số $m$ để đường thẳng $d:y = 2mx + 4$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn $\dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} = - 3$
Có bao nhiêu giá trị nguyên của tham số $m$ để đường thẳng $d:y = 2mx - 2m + 3$ và parabol $\left( P \right):y = {x^2}$ cắt nhau tại hai điểm phân biệt có tọa độ $\left( {{x_1};{y_1}} \right);\left( {{x_2};{y_2}} \right)$ thỏa mãn ${y_1} + {y_2} < 9$
Cho đường thẳng \(d\) :\(y = - 3x + 1\) và parabol : \(\left( P \right)\)\(y = m{x^2}\left( {m \ne 0} \right)\). Tìm \(m\) để \(d\) và \(\left( P \right)\) cắt nhau tại hai điểm \(A\) và \(B\) phân biệt và cùng nằm về một phía đối với trục tung.
Tìm giá trị của tham số $m$ để đường thẳng $d:y = - \dfrac{1}{2}x + m$ và parabol $\left( P \right):y = - \dfrac{1}{4}{x^2}$ cắt nhau tại hai điểm phân biệt có hoành độ ${x_1};{x_2}$ thỏa mãn \(3{x_1} + 5{x_2} = 5\)
Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = \left( {{m^2} + 2} \right)x - {m^2}\). Tìm \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về bên phải trục tung.
Cho parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua điểm \(A\left( {2;4} \right)\) và đường thẳng \(\left( d \right):y = 2(m - 1)x + 2m + 2\) (với \(m\) là tham số). Giá trị của \(m\) để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt là
Cho parabol \(\left( P \right):y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( { - 2;4} \right)\) và tiếp xúc với đồ thị \(\left( d \right)\) của hàm số \(y = 2(m - 1)x - (m - 1)\).Toạ độ tiếp điểm là

















